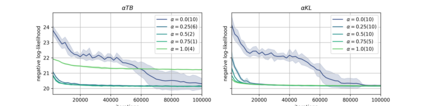
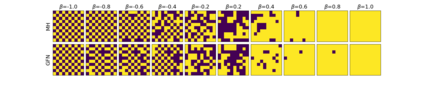
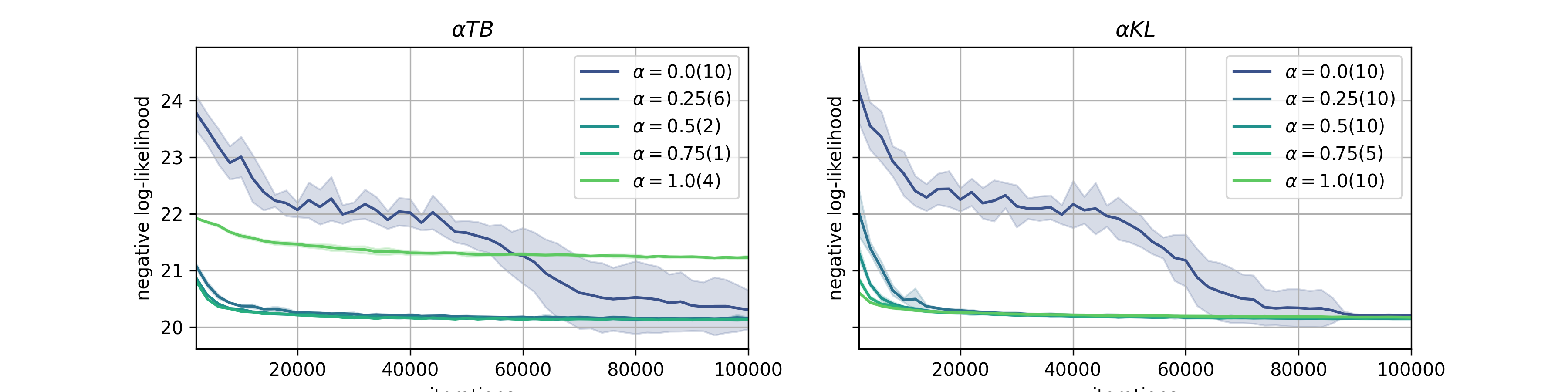
Generative flow networks (GFNs) are a class of models for sequential sampling of composite objects, which approximate a target distribution that is defined in terms of an energy function or a reward. GFNs are typically trained using a flow matching or trajectory balance objective, which matches forward and backward transition models over trajectories. In this work, we define variational objectives for GFNs in terms of the Kullback-Leibler (KL) divergences between the forward and backward distribution. We show that variational inference in GFNs is equivalent to minimizing the trajectory balance objective when sampling trajectories from the forward model. We generalize this approach by optimizing a convex combination of the reverse- and forward KL divergence. This insight suggests variational inference methods can serve as a means to define a more general family of objectives for training generative flow networks, for example by incorporating control variates, which are commonly used in variational inference, to reduce the variance of the gradients of the trajectory balance objective. We evaluate our findings and the performance of the proposed variational objective numerically by comparing it to the trajectory balance objective on two synthetic tasks.
翻译:在这项工作中,我们根据前向和后向分布之间的Kullback-Leibertr(KL)差异来界定GFMs的变式目标。我们表明,GFMs的变式推论相当于在从前向模式取样时尽量减少轨迹平衡目标。我们通过优化逆向和前向KL差异的曲线组合来推广这一方法。这种洞察力表明,变式推论方法可以作为一种手段,用以界定对GFMs进行基因变异流网络培训的更普遍的目标,例如,采用在变式推论中常用的控制变式,以减少轨迹平衡目标的梯度差异。我们通过将逆向和前向KL差异的曲线组合优化来评估我们的调查结果和拟议变异目标的绩效,将之与两个合成任务的目标轨迹平衡目标进行比较。