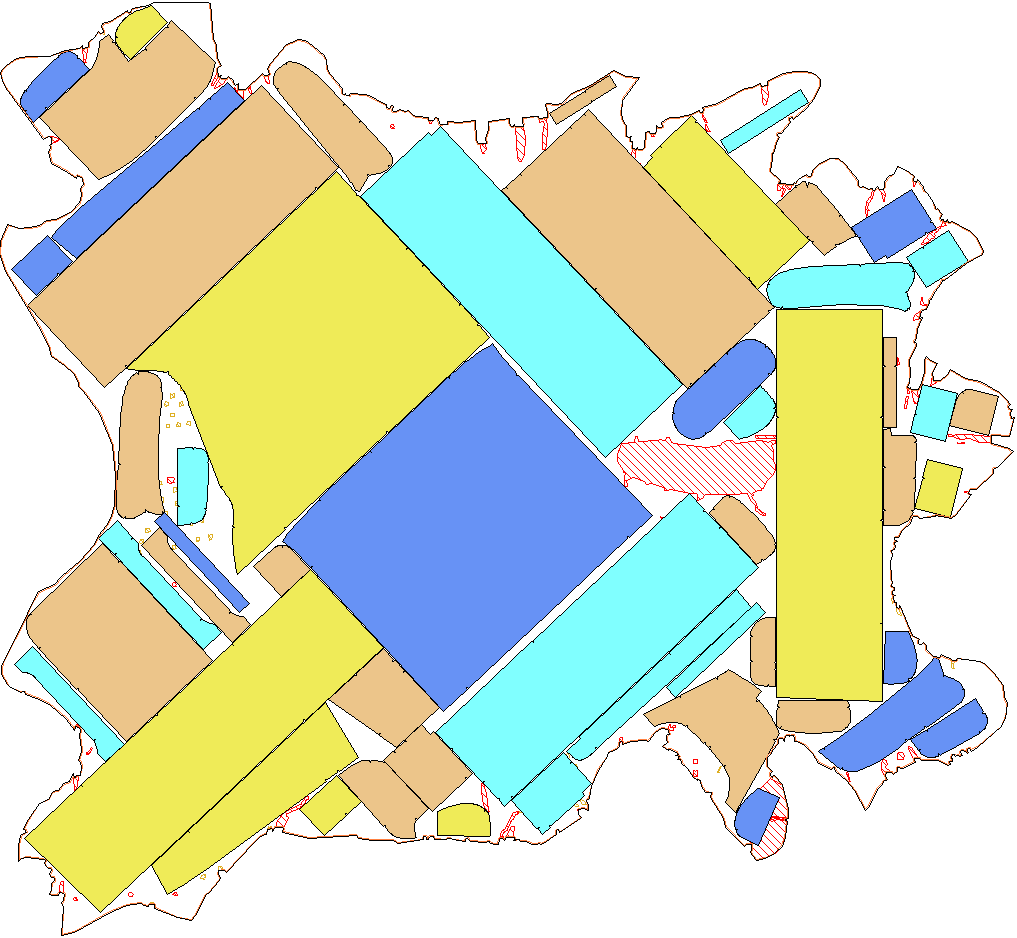
The aim in packing problems is to decide if a given set of pieces can be placed inside a given container. A packing problem is defined by the types of pieces and containers to be handled, and the motions that are allowed to move the pieces. The pieces must be placed so that in the resulting placement, they are pairwise interior-disjoint. We establish a framework which enables us to show that for many combinations of allowed pieces, containers and motions, the resulting problem is $\exists \mathbb{R}$-complete. This means that the problem is equivalent (under polynomial time reductions) to deciding whether a given system of polynomial equations and inequalities with integer coefficients has a real solution. We consider packing problems where only translations are allowed as the motions, and problems where arbitrary rigid motions are allowed, i.e., both translations and rotations. When rotations are allowed, we show that it is an $\exists \mathbb{R}$-complete problem to decide if a set of convex polygons, each of which has at most $7$ corners, can be packed into a square. Restricted to translations, we show that the following problems are $\exists \mathbb{R}$-complete: (i) pieces bounded by segments and hyperbolic curves to be packed in a square, and (ii) convex polygons to be packed in a container bounded by segments and hyperbolic curves.
翻译:包装问题的目的是要决定某一组碎片是否可以放置在给定的容器内。 包装问题由要处理的碎片和容器的类型以及允许移动碎片的动作来定义。 必须放置这些碎片, 以便在由此造成的放置位置中, 它们是配对的内部脱节。 我们建立一个框架, 使我们能够显示对于许多允许的碎片、 容器和运动组合来说, 由此产生的问题是 $\ expences\ mathbb{R}$- 完整的。 这意味着问题相当于( 在多边时间缩减下) 确定一个特定多式方和偏差的系统是否具有真正的解决方案。 我们考虑的包装问题, 只有翻译才被允许作为运动, 以及任意的僵硬动作被允许的问题, 即翻译和旋转。 当允许旋转时, 我们显示它是一个 $\ deceptions \ mathbb{R} $- 完整的问题。 这意味着要决定一组正统多边形多边形( 每一类都有最多7美元角的) 和折形区域的曲线是否可以包装成一个正版 。 (restricr=r=real) 折成一个正形的折成一个正形的折成一个正形的折形。