Dynamic mean field programming

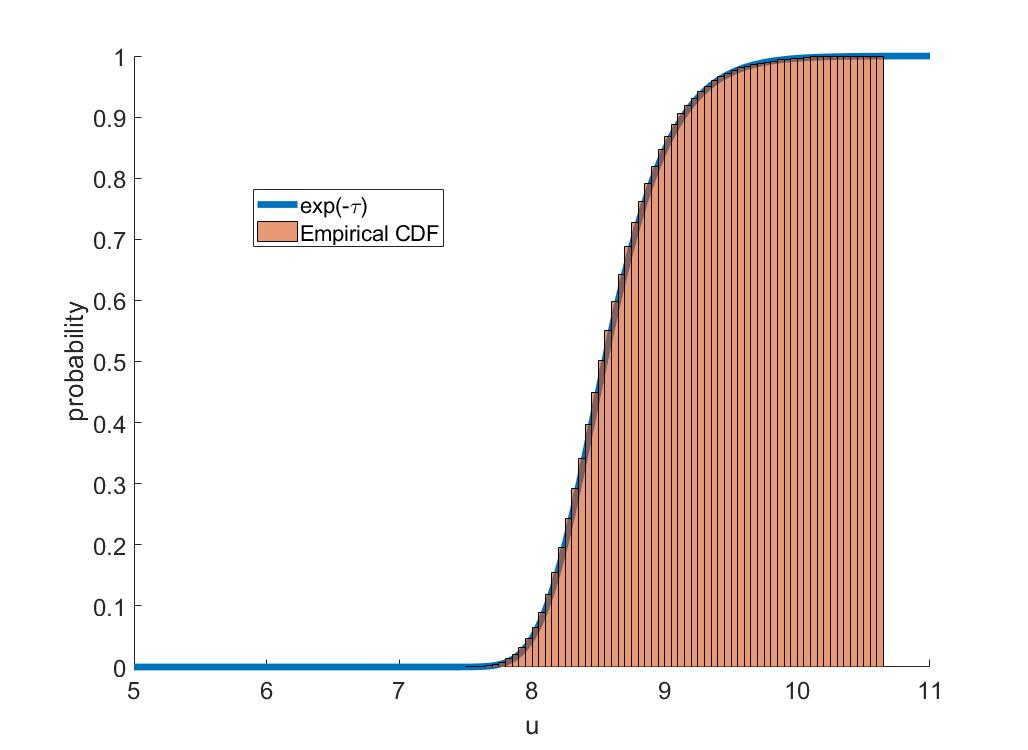
A dynamic mean field theory is developed for model based Bayesian reinforcement learning in the large state space limit. In an analogy with the statistical physics of disordered systems, the transition probabilities are interpreted as couplings, and value functions as deterministic spins, and thus the sampled transition probabilities are considered to be quenched random variables. The results reveal that, under standard assumptions, the posterior over Q-values is asymptotically independent and Gaussian across state-action pairs, for infinite horizon problems. The finite horizon case exhibits the same behaviour for all state-actions pairs at each time but has an additional correlation across time, for each state-action pair. The results also hold for policy evaluation. The Gaussian statistics can be computed from a set of coupled mean field equations derived from the Bellman equation, which we call dynamic mean field programming (DMFP). For Q-value iteration, approximate equations are obtained by appealing to extreme value theory, and closed form expressions are found in the independent and identically distributed case. The Lyapunov stability of these closed form equations is studied.