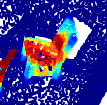
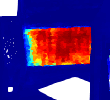
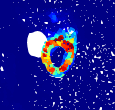
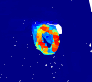
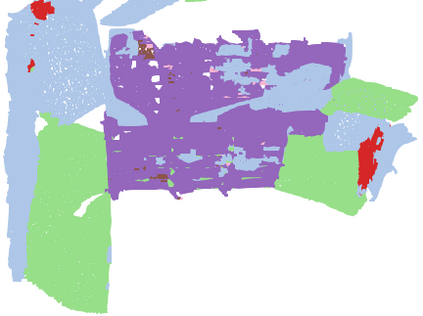
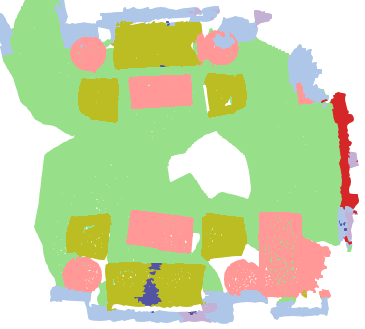
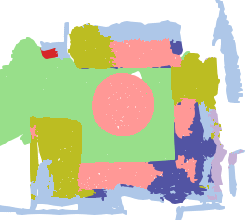
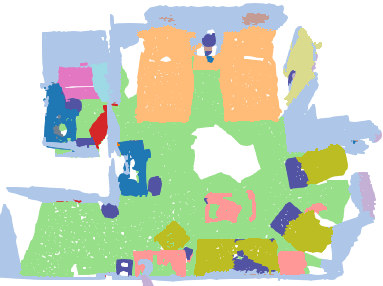
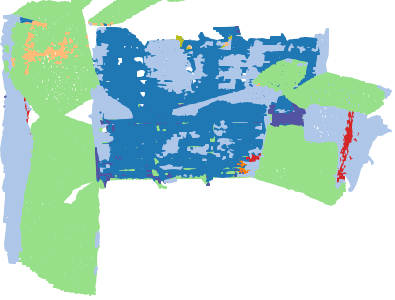
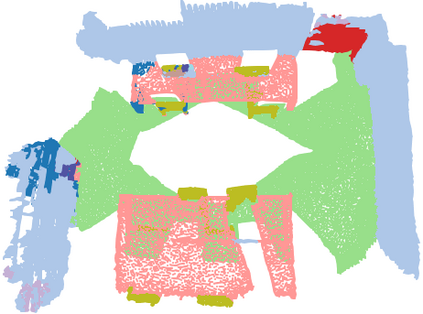
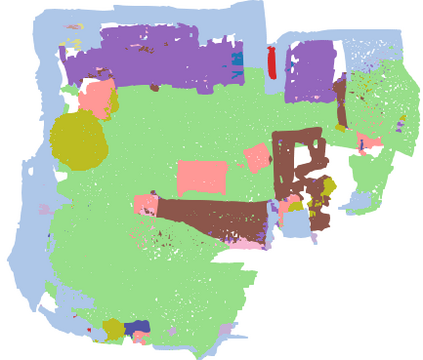
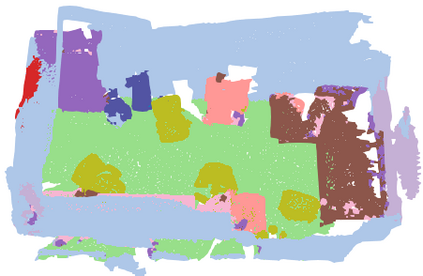
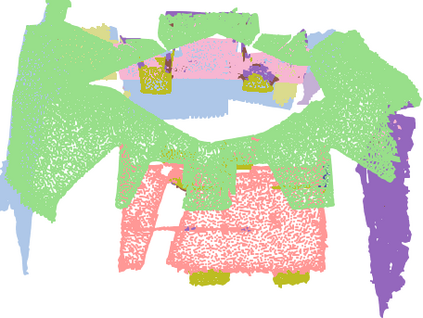
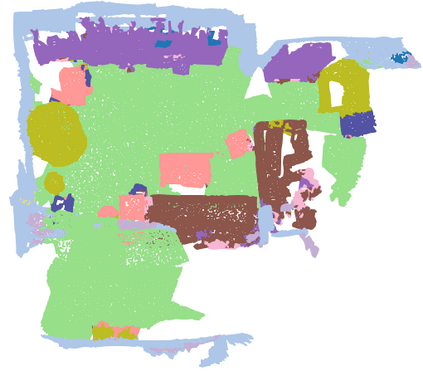
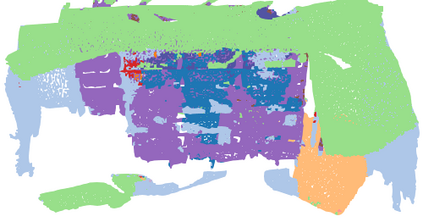
We investigate transductive zero-shot point cloud semantic segmentation in this paper, where unseen class labels are unavailable during training. Actually, the 3D geometric elements are essential cues to reason the 3D object type. If two categories share similar geometric primitives, they also have similar semantic representations. Based on this consideration, we propose a novel framework to learn the geometric primitives shared in seen and unseen categories' objects, where the learned geometric primitives are served for transferring knowledge from seen to unseen categories. Specifically, a group of learnable prototypes automatically encode geometric primitives via back-propagation. Then, the point visual representation is formulated as the similarity vector of its feature to the prototypes, which implies semantic cues for both seen and unseen categories. Besides, considering a 3D object composed of multiple geometric primitives, we formulate the semantic representation as a mixture-distributed embedding for the fine-grained match of visual representation. In the end, to effectively learn the geometric primitives and alleviate the misclassification issue, we propose a novel unknown-aware infoNCE loss to align the visual and semantic representation. As a result, guided by semantic representations, the network recognizes the novel object represented with geometric primitives. Extensive experiments show that our method significantly outperforms other state-of-the-art methods in the harmonic mean-intersection-over-union (hIoU), with the improvement of 17.8%, 30.4% and 9.2% on S3DIS, ScanNet and SemanticKITTI datasets, respectively. Codes will be released.
翻译:我们在本文中调查了感官零光点云的语义分解, 培训期间无法找到隐形类标签。 事实上, 3D 几何元素是解释 3D 对象类型的基本线索。 如果两个类别拥有相似的几何原始元素, 它们也有相似的语义表示。 基于这一考虑, 我们提出一个新的框架来学习在可见和看不见类别中共享的几何原始元素, 在那里, 学习过的几何原始元素可以用来将知识从可见到看不见的类别传递到不可见的类别。 具体地说, 一组可学习的原型通过反向分析自动将几何原始元素编码自动编码。 然后, 点直观表达作为其特性与原型相似的矢量矢量矢量矢量矢量矢量矢量矢量。 此外, 考虑到一个由多几何原始元素组成的3D对象, 我们将语义表示的语义表达方式作为精度分解的混凝固的混合嵌合体, 视觉表达方式将是: 有效学习几何直径直径直径直径直径直径直径直径直径直径直径直径, 。 我们用直径直径直径直径直径直径直径直径直径直径直径直径解的图解图解解解解解解解解解解的图解解解解的解解解方法将分解算法将分解算出, 。