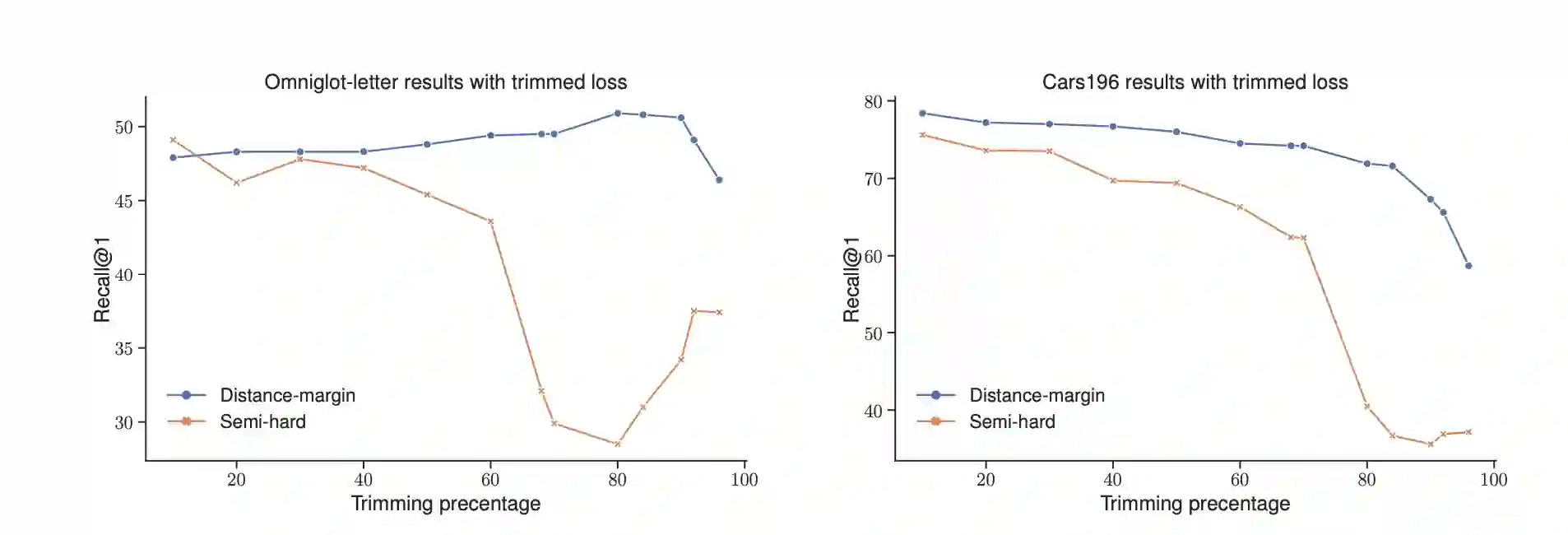
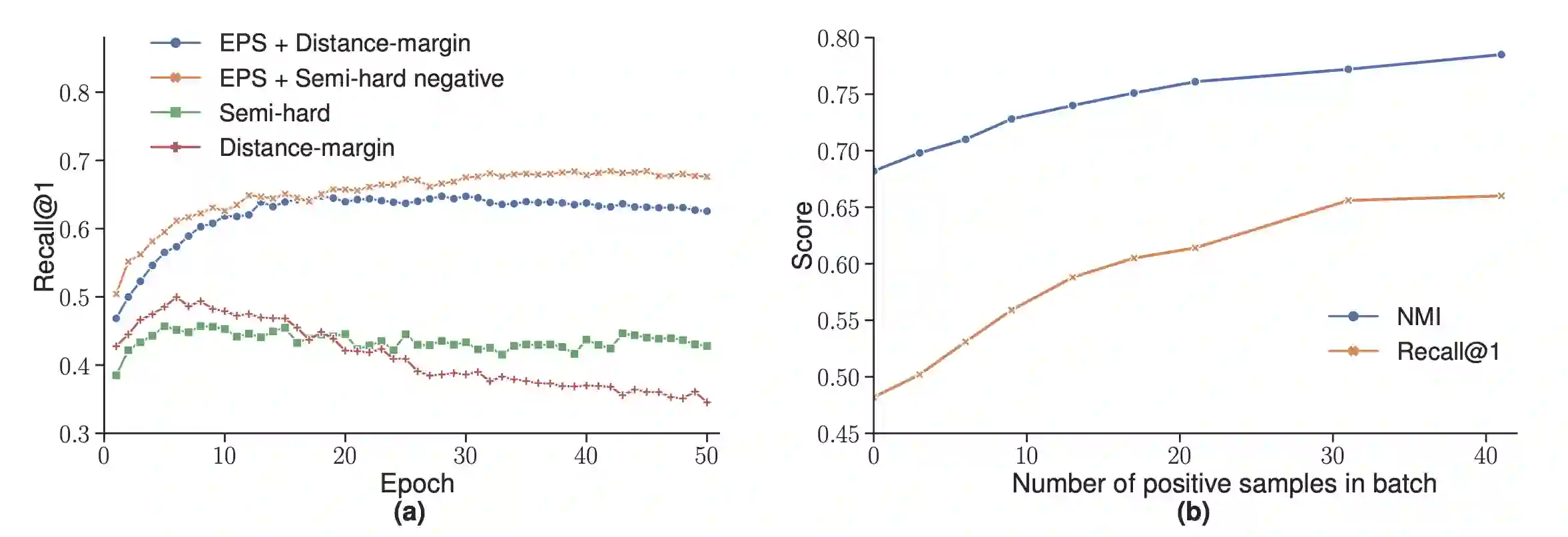
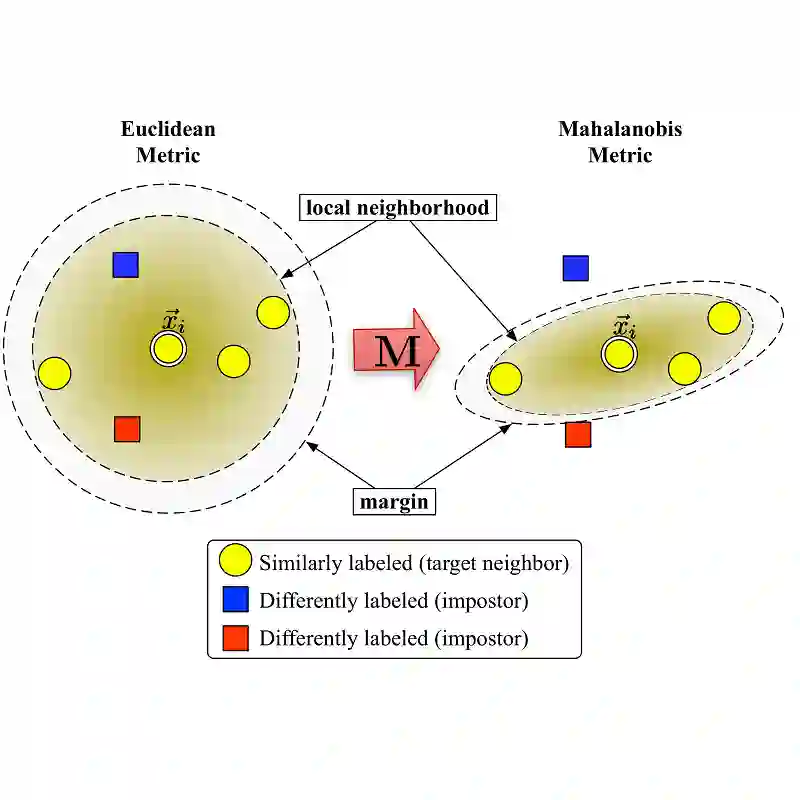
Metric learning seeks perceptual embeddings where visually similar instances are close and dissimilar instances are apart, but learned representations can be sub-optimal when the distribution of intra-class samples is diverse and distinct sub-clusters are present. Although theoretically with optimal assumptions, margin-based losses such as the triplet loss and margin loss have a diverse family of solutions. We theoretically prove and empirically show that under reasonable noise assumptions, margin-based losses tend to project all samples of a class with various modes onto a single point in the embedding space, resulting in a class collapse that usually renders the space ill-sorted for classification or retrieval. To address this problem, we propose a simple modification to the embedding losses such that each sample selects its nearest same-class counterpart in a batch as the positive element in the tuple. This allows for the presence of multiple sub-clusters within each class. The adaptation can be integrated into a wide range of metric learning losses. The proposed sampling method demonstrates clear benefits on various fine-grained image retrieval datasets over a variety of existing losses; qualitative retrieval results show that samples with similar visual patterns are indeed closer in the embedding space.
翻译:虽然理论上有最佳假设,但三重损失和差值损失等基于差值的损失有多种解决办法。我们从理论上证明并经验上表明,在合理的噪音假设下,以差值为基础的损失往往将不同模式的所有类别样本都投射到嵌入空间的单一点上,从而导致舱级崩溃,通常造成空间分类或检索错误。为了解决这一问题,我们建议对嵌入损失进行简单修改,这样,每个样本选择最近的同级对应方,分批选择正值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值,从而可以将多个子级值值值值值值值值值值值值值值值值值值值值值损失纳入。提议的取样方法表明,各种细微图像检索数据集对各种现有损失都有明显的好处;定性检索结果显示,在嵌入空间时,具有类似视觉模式的样本确实接近。