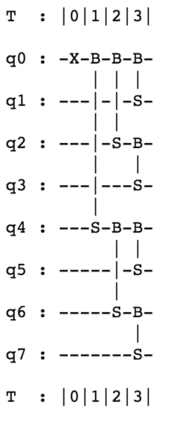
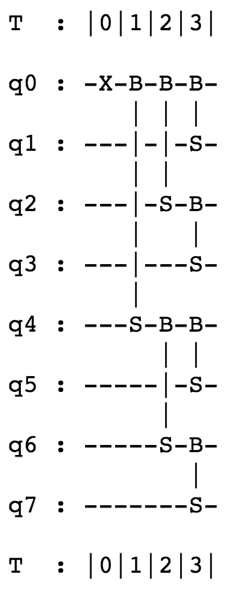
We introduce a new approach for quantum linear algebra based on quantum subspace states and present three new quantum machine learning algorithms. The first is a quantum determinant sampling algorithm that samples from the distribution $\Pr[S]= det(X_{S}X_{S}^{T})$ for $|S|=d$ using $O(nd)$ gates and with circuit depth $O(d\log n)$. The state of art classical algorithm for the task requires $O(d^{3})$ operations \cite{derezinski2019minimax}. The second is a quantum singular value estimation algorithm for compound matrices $\mathcal{A}^{k}$, the speedup for this algorithm is potentially exponential. It decomposes a $\binom{n}{k}$ dimensional vector of order-$k$ correlations into a linear combination of subspace states corresponding to $k$-tuples of singular vectors of $A$. The third algorithm reduces exponentially the depth of circuits used in quantum topological data analysis from $O(n)$ to $O(\log n)$. Our basic tool are quantum subspace states, defined as $|Col(X)\rangle = \sum_{S\subset [n], |S|=d} det(X_{S}) |S\rangle$ for matrices $X \in \mathbb{R}^{n \times d}$ such that $X^{T} X = I_{d}$, that encode $d$-dimensional subspaces of $\mathbb{R}^{n}$. We develop two efficient state preparation techniques, the first using Givens circuits uses the representation of a subspace as a sequence of Givens rotations, while the second uses efficient implementations of unitaries $\Gamma(x) = \sum_{i} x_{i} Z^{\otimes (i-1)} \otimes X \otimes I^{n-i}$ with $O(\log n)$ depth circuits that we term Clifford loaders.
翻译:我们引入基于量子空间状态的量子线性变数新方法, 并推出三种新的量子机器学习算法。 首先是量子决定因素算法, 使用 $O( d) 门和电路深度 $O( d\log n) 来对量子线性变数进行取样。 任务的最新古典算法需要 $( d% 3} 美元 操作 =cite{derezinski2019minmax} 。 第二个是 从 $\ Pr[ S] = d( d) 美元, 这个算法的加速值算法可能是指数的。 它将一个 $( binom{ X} 美元 美元) 的量子矢量矢量结合成 $( t) 美元( 美元) 美元( = *% 立方美元 美元 = 美元 美元。 (x=xxxxxxx) 数据分析中的量表数据深度, 以 $(n) R$( = 美元= 美元) sal= 美元( sal= a stal) a stals deals deals deals) a.