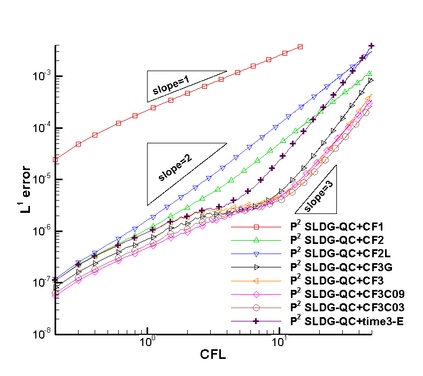
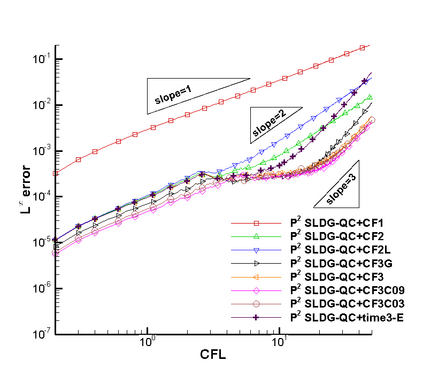
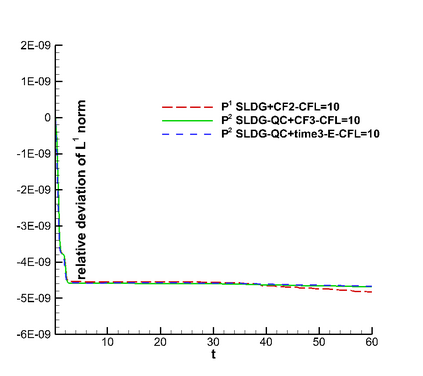
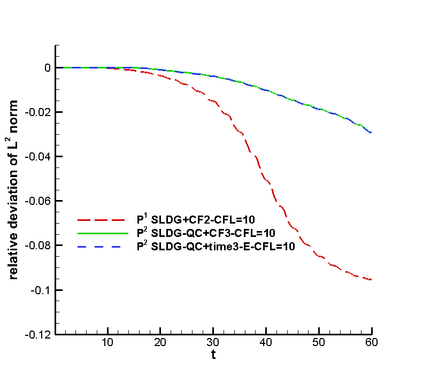
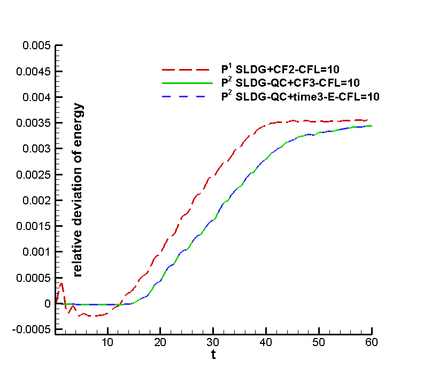
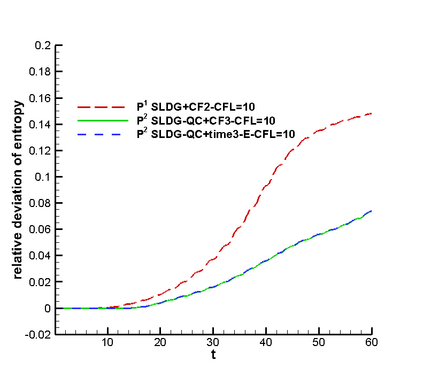
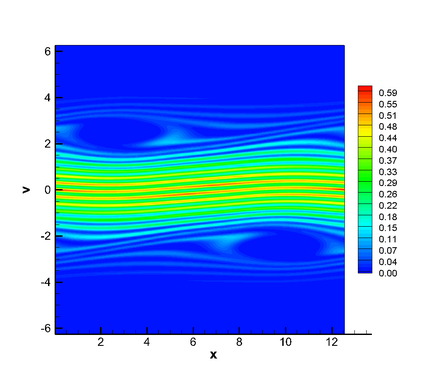
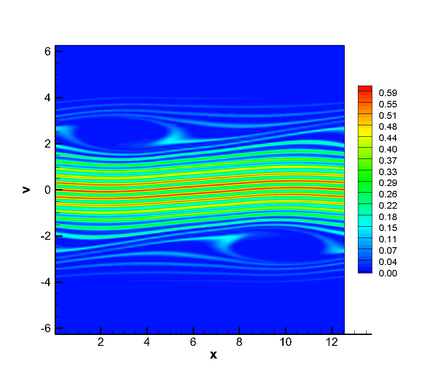
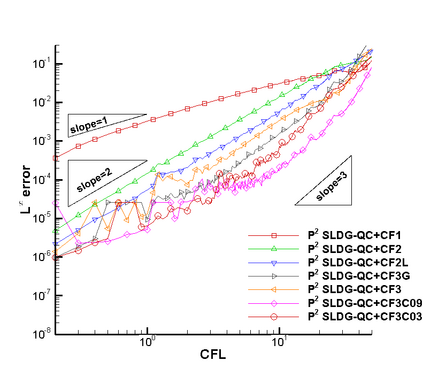
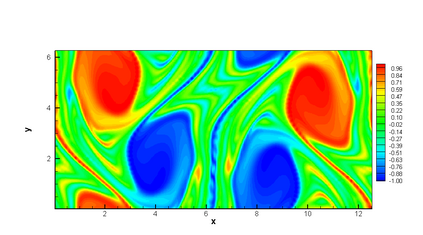
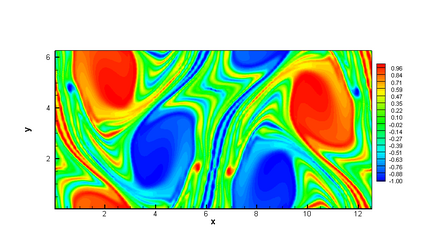
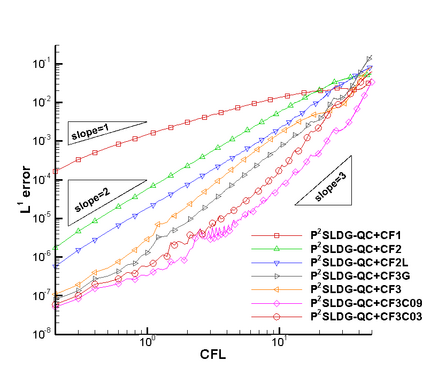
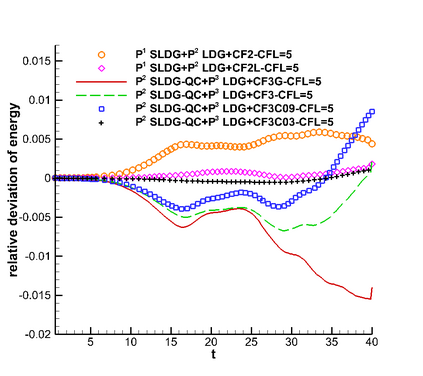
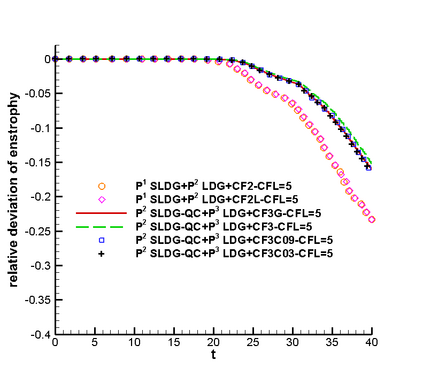
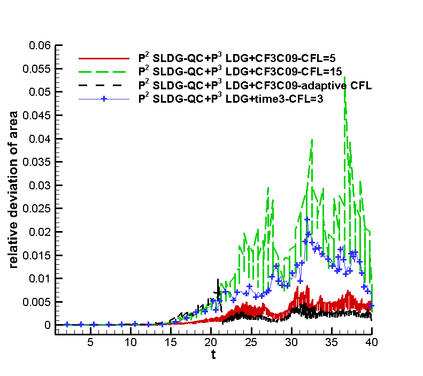
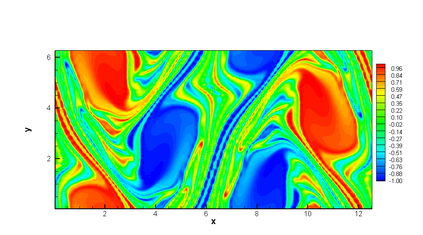
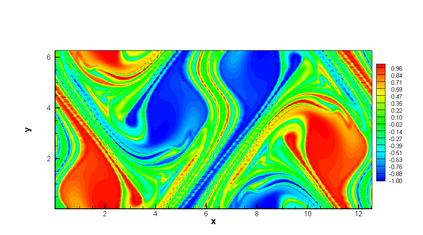
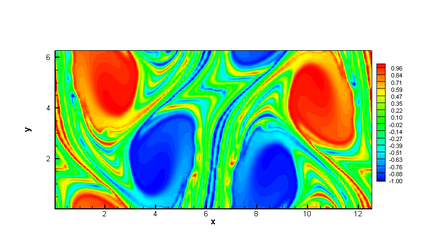
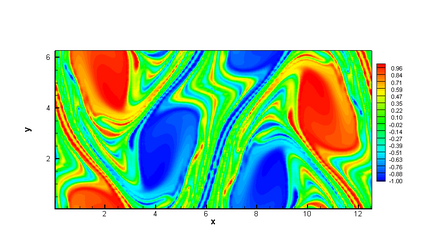
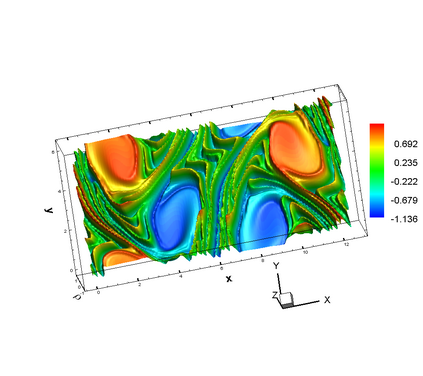
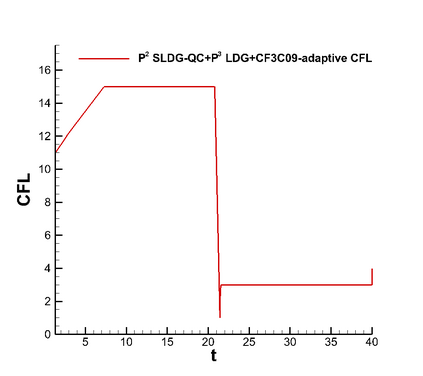
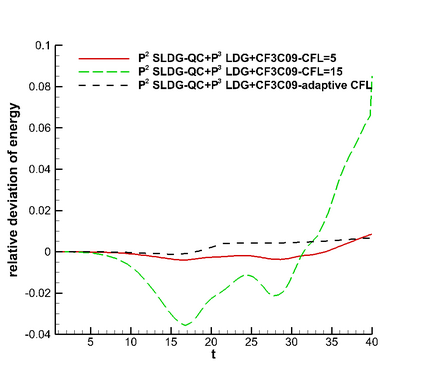
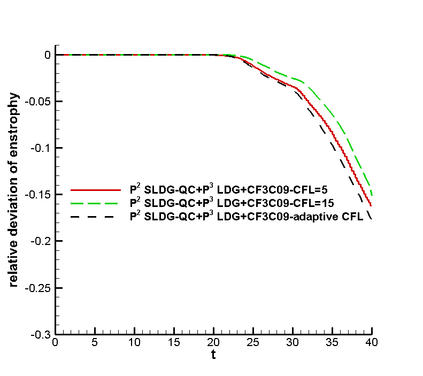
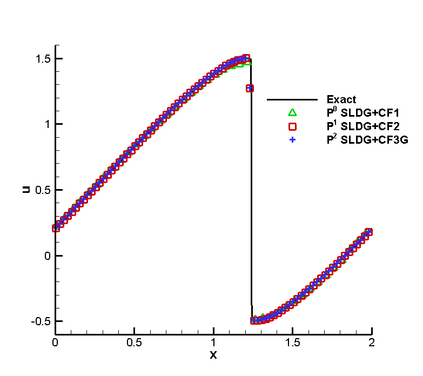
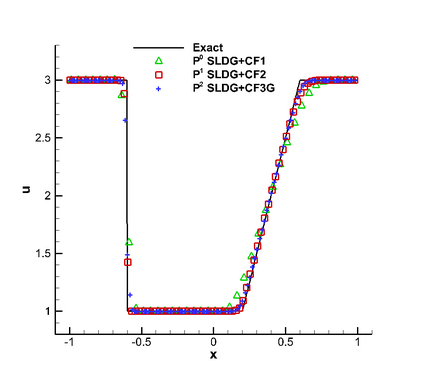
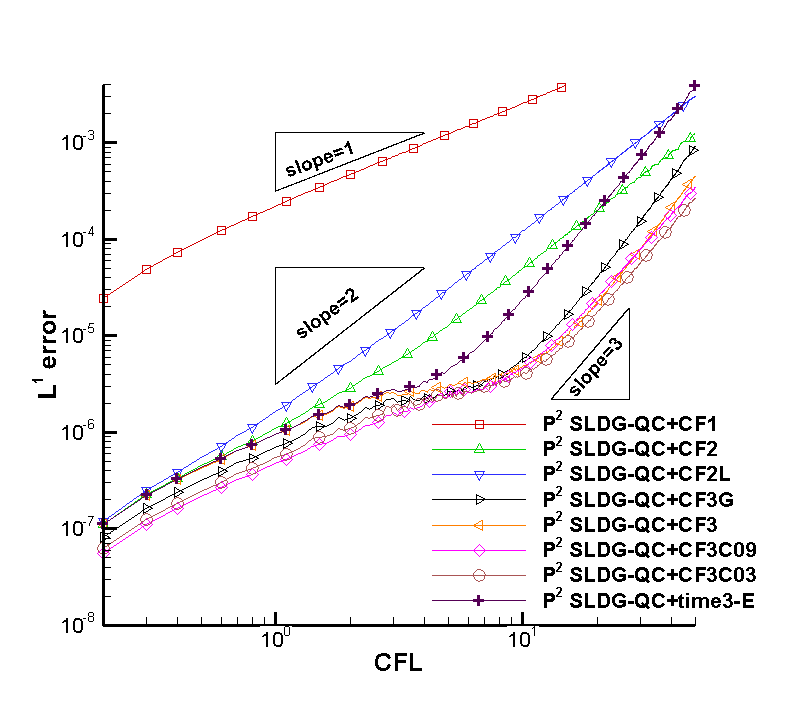
In this paper, we propose a semi-Lagrangian discontinuous Galerkin method coupled with Runge-Kutta exponential integrators (SLDG-RKEI) for nonlinear Vlasov dynamics. The commutator-free Runge-Kutta (RK) exponential integrators (EI) were proposed by Celledoni, et al. (FGCS, 2003). In the nonlinear transport setting, the RKEI can be used to decompose the evolution of the nonlinear transport into a composition of a sequence of linearized dynamics. The resulting linearized transport equations can be solved by the semi-Lagrangian (SL) discontinuous Galerkin (DG) method proposed in Cai, et al. (JSC, 2017). The proposed method can achieve high order spatial accuracy via the SLDG framework, and high order temporal accuracy via the RK EI. Due to the SL nature, the proposed SLDG-RKEI method is not subject to the CFL condition, thus they have the potential in using larger time-stepping sizes than those in the Eulerian approach. Inheriting advantages from the SLDG method, the proposed SLDG-RKEI schemes are mass conservative, positivity-preserving, have no dimensional splitting error, perform well in resolving complex solution structures, and can be evolved with adaptive time-stepping sizes. We show the performance of the SLDG-RKEI algorithm by classical test problems for the nonlinear Vlasov-Poisson system, as well as the Guiding center Vlasov model. Though that it is not our focus of this paper to explore the SLDG-RKEI scheme for nonlinear hyperbolic conservation laws that develop shocks, we show some preliminary results on schemes' performance on the Burgers' equation.
翻译:在本文中,我们提出了一个半Lagrangian不连续的Galerkin 方法,加上对非线性Vlasov动态的Runge-Kutta指数化集成器(SLDG-RKEI) 。 Celledoni 等人(FGCS,2003年) 提出了无通向的Lunge-Kutta指数化集成器(EI) 。在非线性运输环境中,RKEI可以用来将非线性运输的演变分解成线性动态序列的组合。由此产生的线性运输方程式(SLDG-RKERI) 由半Lagrangian(SLSG,2017年) 的不连续性Gerkin(DGG) 方法来解决。 拟议的方法可以通过SLGGF框架实现高端空间精确度,而通过RK EI 高端时间性能精确性能。由于SLLDG-RI 方法的性质, 拟议的SLDG-RI 方法可以不受CLI 状态的制约,因此它们有可能使用更长时间的不平稳的平流性平流的平流的平流性规模,而显示SDG- RDFI 方法的平面性平面性能的平流法 显示Sulation 的平局的平流的平流性能的平向的平面性方法。