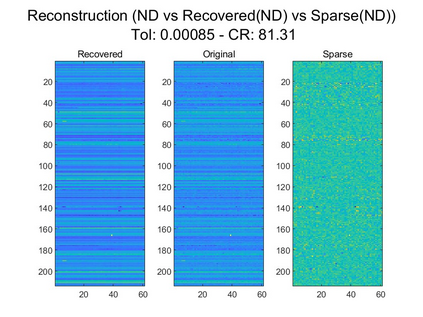
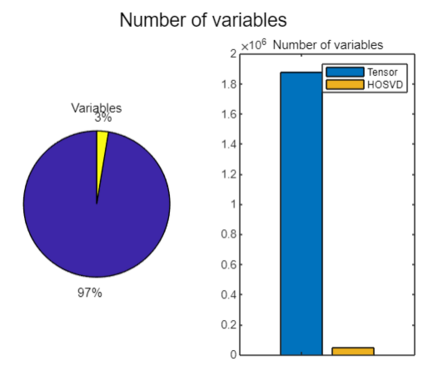
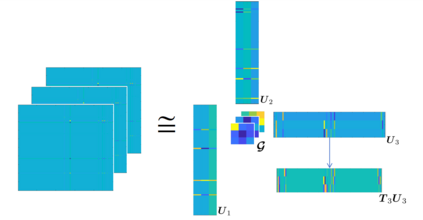
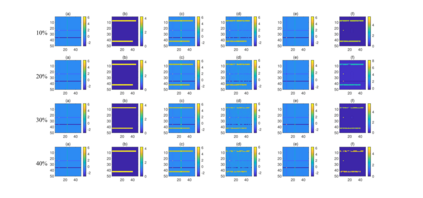
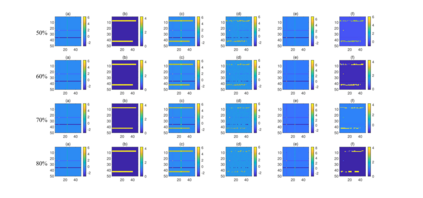
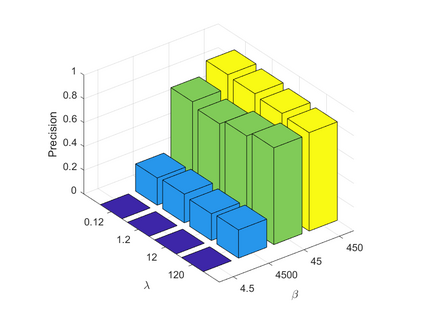
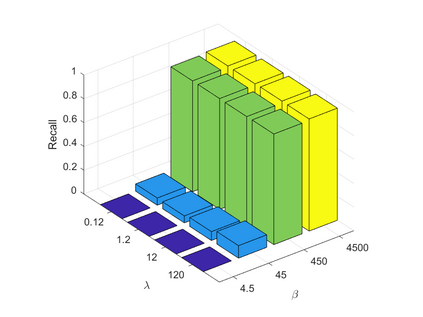
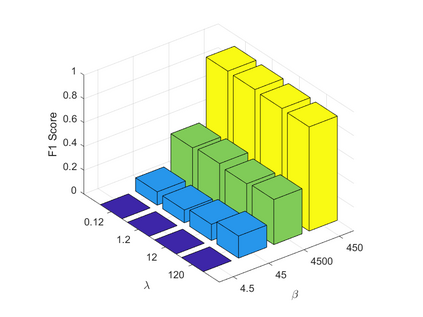
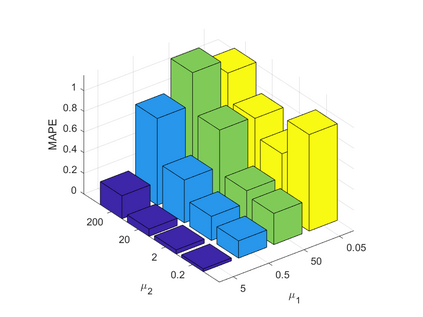
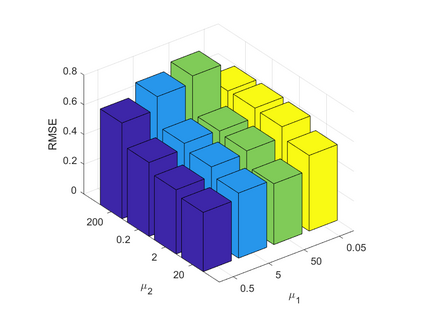
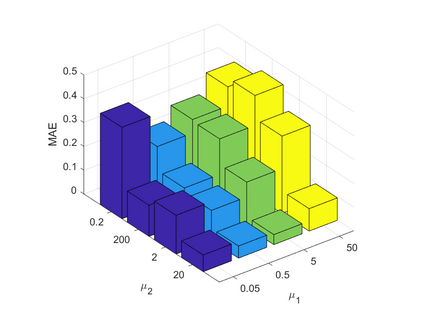
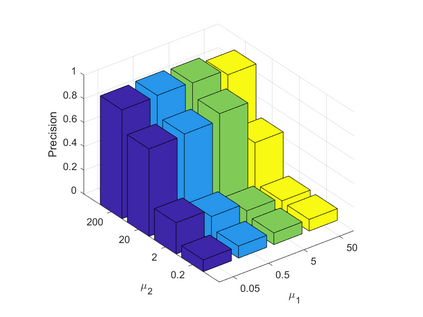
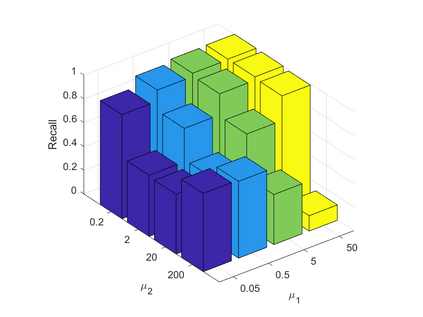
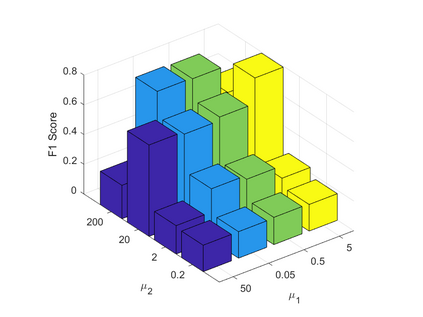
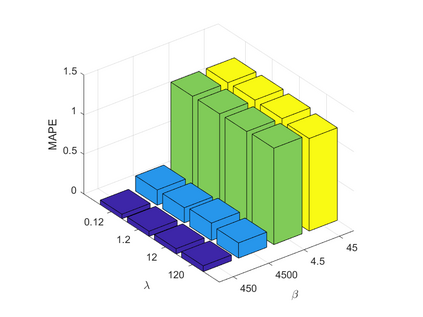
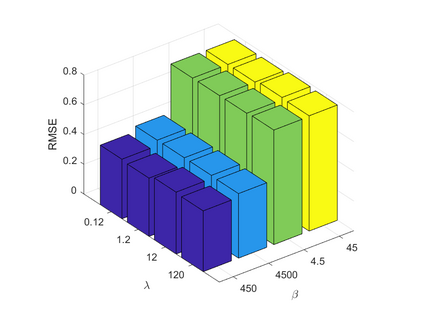
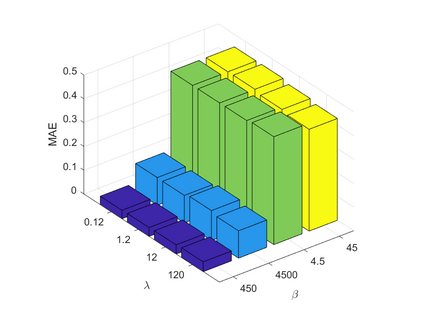
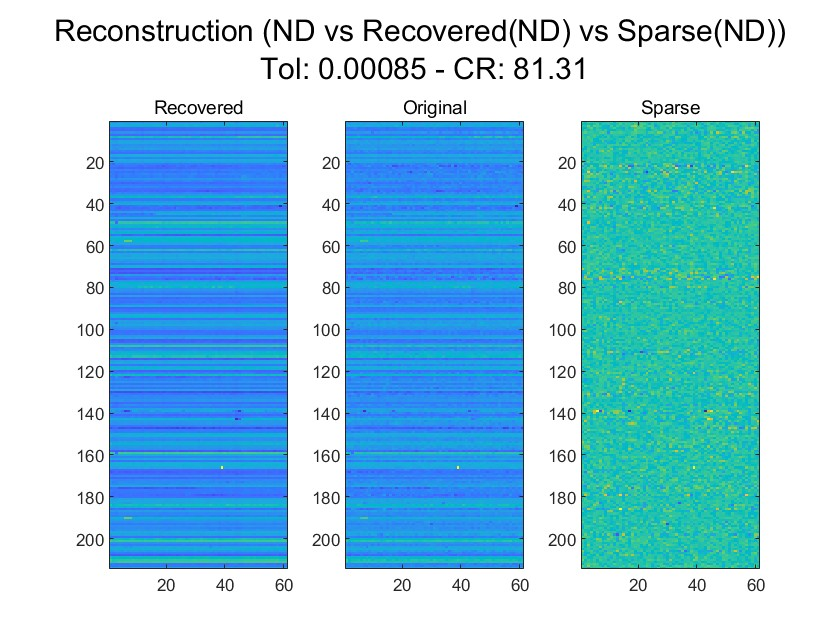
Spatiotemporal traffic time series, such as traffic speed data, collected from sensing systems are often incomplete, with considerable corruption and large amounts of missing values. A vast amount of data conceals implicit data structures, which poses significant challenges for data recovery issues, such as mining the potential spatio-temporal correlations of data and identifying abnormal data. In this paper, we propose a Tucker decomposition-based sparse low-rank high-order tensor optimization model (TSLTO) for data imputation and anomaly diagnosis. We decompose the traffic tensor data into low-rank and sparse tensors, and establish a sparse low-rank high-order tensor optimization model based on Tucker decomposition. By utilizing tools of non-smooth analysis for tensor functions, we explore the optimality conditions of the proposed tensor optimization model and design an ADMM optimization algorithm for solving the model. Finally, numerical experiments are conducted on both synthetic data and a real-world dataset: the urban traffic speed dataset of Guangzhou. Numerical comparisons with several representative existing algorithms demonstrate that our proposed approach achieves higher accuracy and efficiency in traffic flow data recovery and anomaly diagnosis tasks.
翻译:暂无翻译