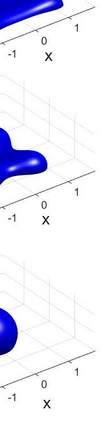
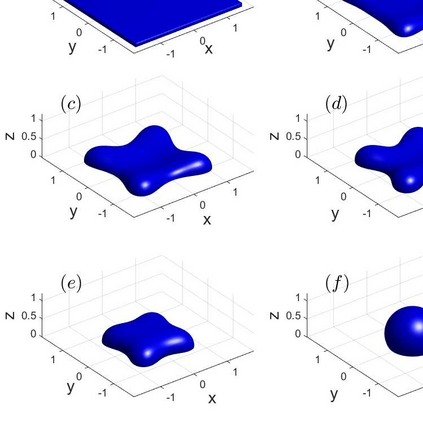
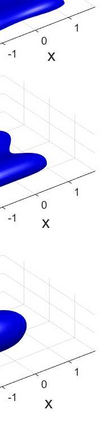
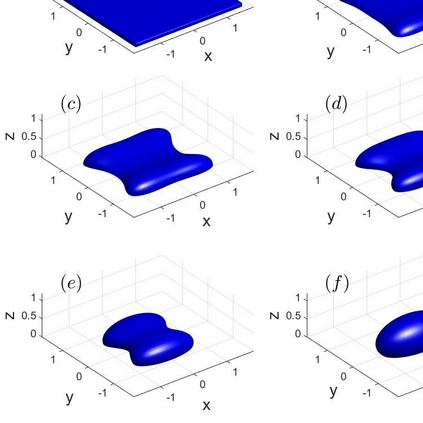
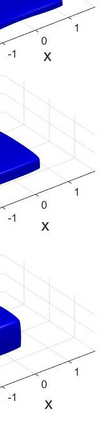
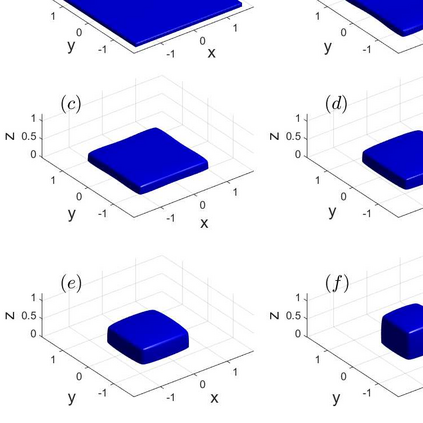
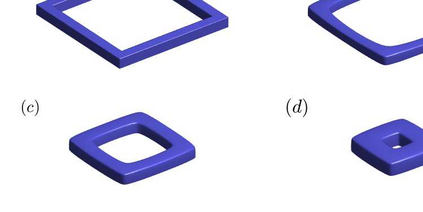
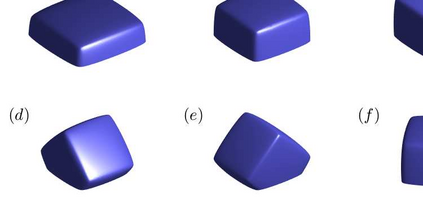
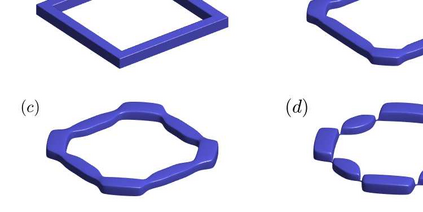
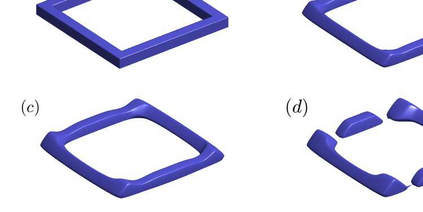
We propose an accurate and energy-stable parametric finite element method for solving the sharp-interface continuum model of solid-state dewetting in three-dimensional space. The model describes the motion of the film\slash vapor interface with contact line migration and is governed by the surface diffusion equation with proper boundary conditions at the contact line. We present a new weak formulation for the problem, in which the interface and its contact line are evolved simultaneously. By using piecewise linear elements in space and backward Euler in time, we then discretize the weak formulation to obtain a fully discretized parametric finite element approximation. The resulting numerical method is shown to be well-posed and unconditionally energy-stable. Furthermore, the numerical method is extended for solving the sharp interface model of solid-state dewetting with anisotropic surface energies in the Riemmanian metric form. Numerical results are reported to show the convergence and efficiency of the proposed numerical method as well as the anisotropic effects on the morphological evolution of thin films in solid-state dewetting.
翻译:我们提出了一种精确且能控的参数性要素方法,用以解决三维空间固态降温的锐利界面连续模型,该模型描述了与接触线迁移的胶片/斜线蒸发界面的动态,并受在接触线上具有适当边界条件的表面扩散方程式的制约。我们为问题提出了一种新的微弱的配方,其中界面及其接触线同时演进。通过在空间和后向电极中使用细微线性元素,我们随后将微弱的配方分解,以获得完全离散的参数性临界元素近似。由此得出的数值方法被证明是妥善保存和无条件的能量稳定。此外,数字方法被扩展,用于解决固态降温与Riemman光学形态中的厌异地表能的锐利界面模式。据报告,数字结果显示拟议的数字方法的趋同和效率,以及对于固态脱湿状态薄薄膜的形态演进产生的异性影响。