Analysis of a local discontinuous Galerkin scheme for fractional Korteweg-de Vries equation

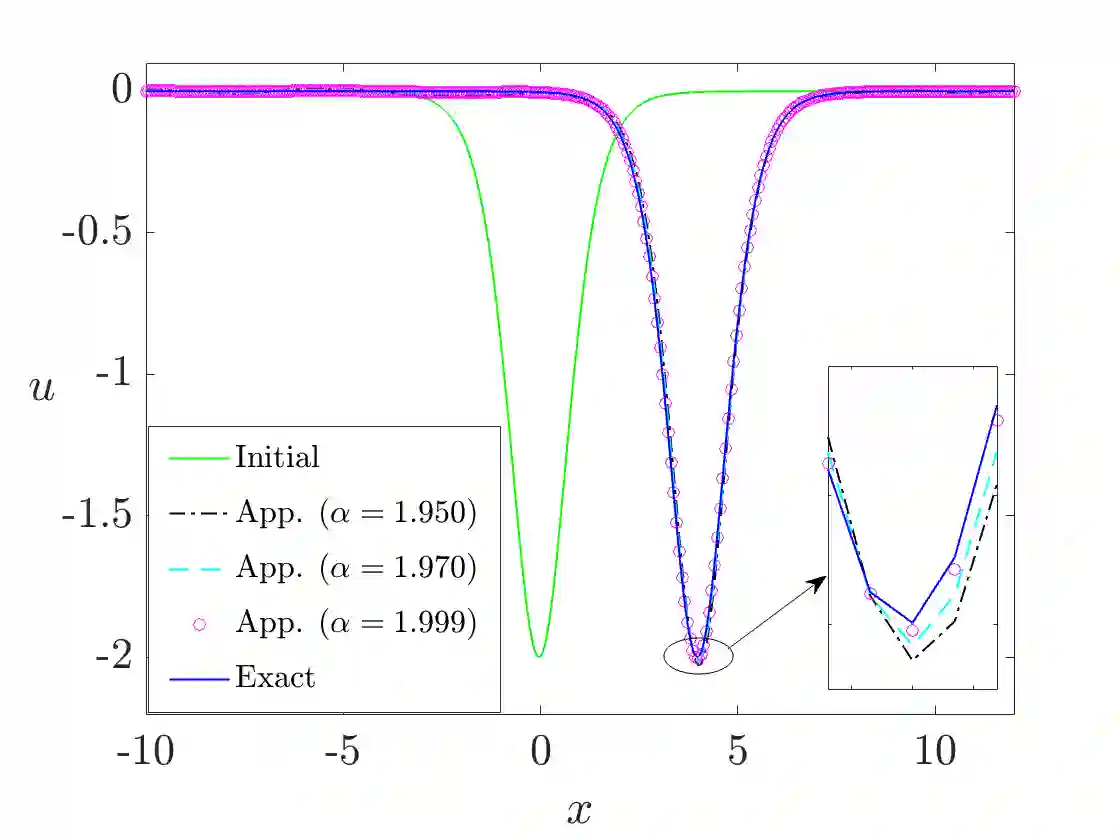
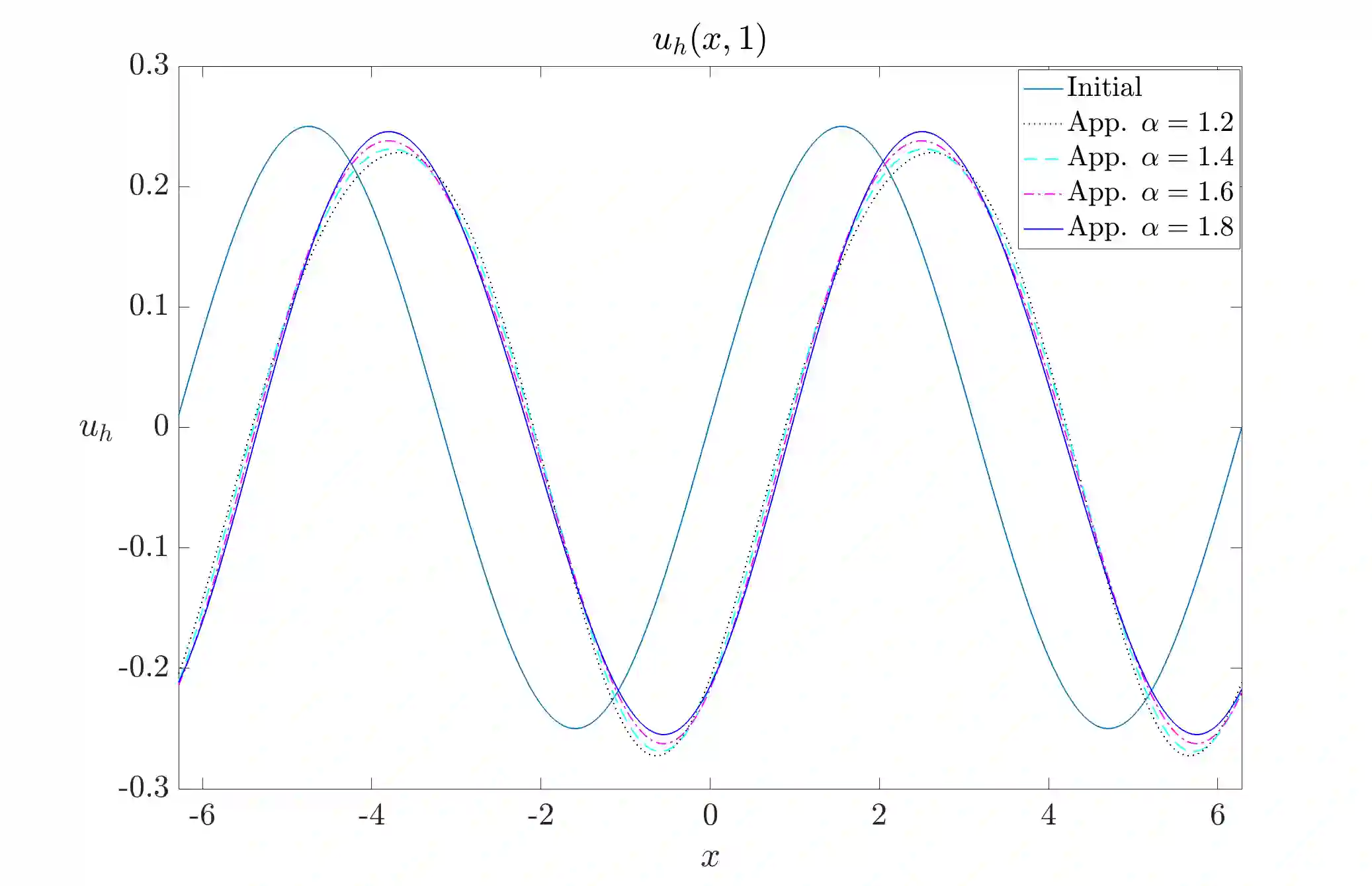
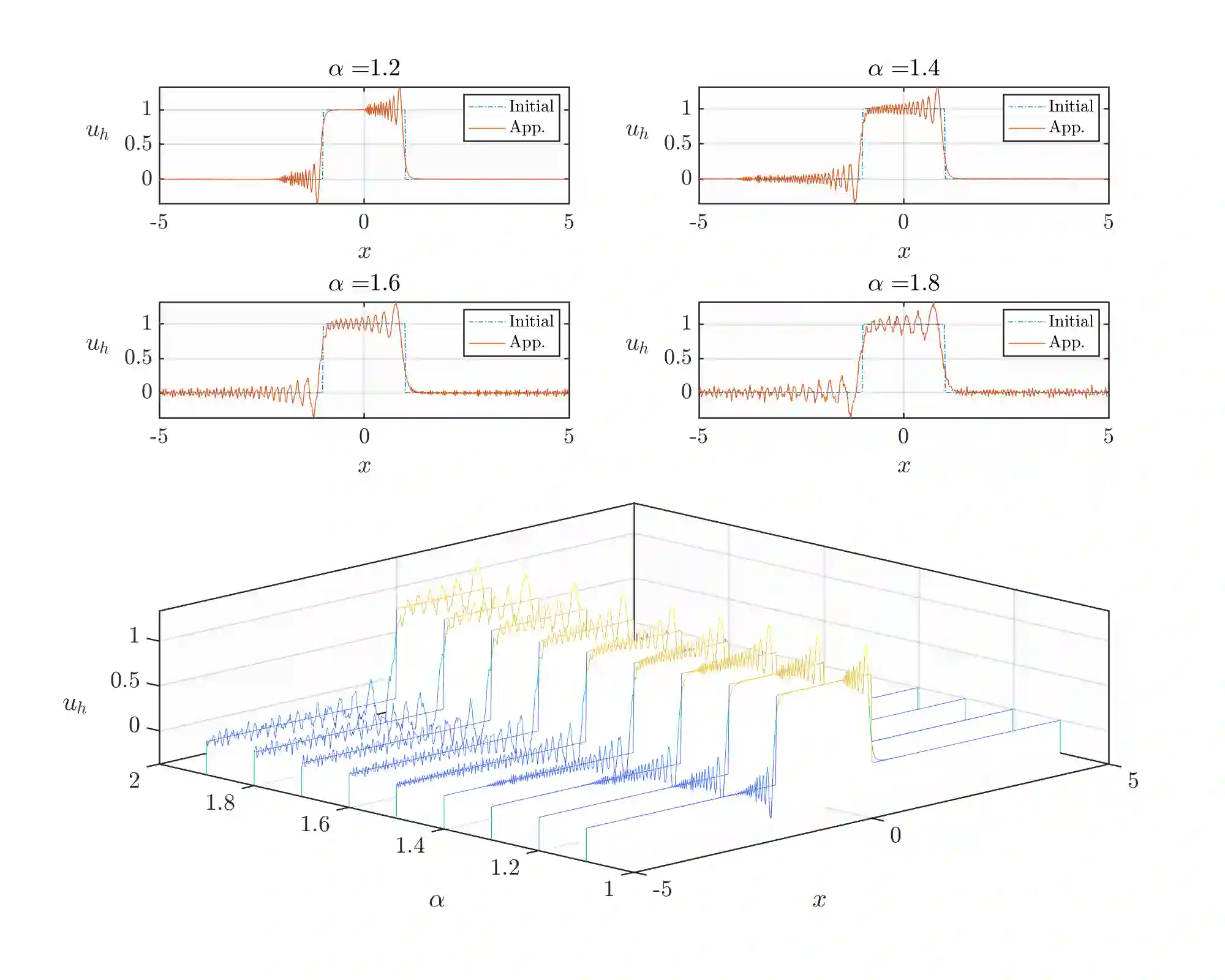
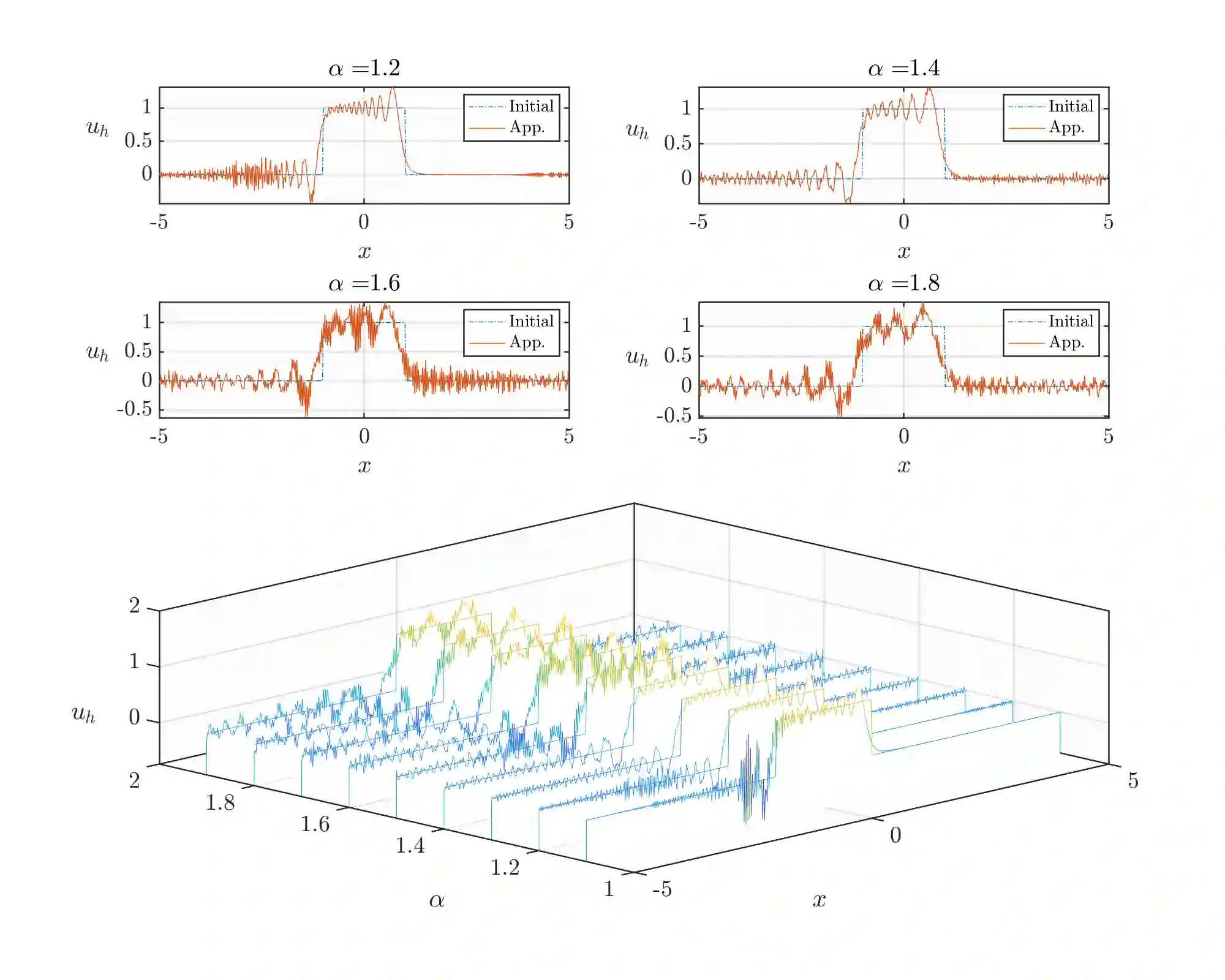
We propose a local discontinuous Galerkin (LDG) method for the fractional Korteweg-de Vries (KdV) equation, involving the fractional Laplacian with exponent $\alpha \in (1,2)$ in one and multiple space dimensions. By decomposing the fractional Laplacian into first-order derivatives and a fractional integral, we prove the $L^2$-stability of the semi-discrete LDG scheme incorporating suitable interface and boundary fluxes. We derive the optimal error estimate for linear flux and demonstrate an error estimate with an order of convergence $\mathcal{O}(h^{k+\frac{1}{2}})$ for general nonlinear flux utilizing the Gauss-Radau projections. Moreover, we extend the stability and error analysis to the multiple space dimensional case. Additionally, we discretize time using the Crank-Nicolson method to devise a fully discrete stable LDG scheme, and obtain a similar order error estimate as in the semi-discrete scheme. Numerical illustrations are provided to demonstrate the efficiency of the scheme, confirming an optimal order of convergence.