Equilibrium and non-Equilibrium regimes in the learning of Restricted Boltzmann Machines

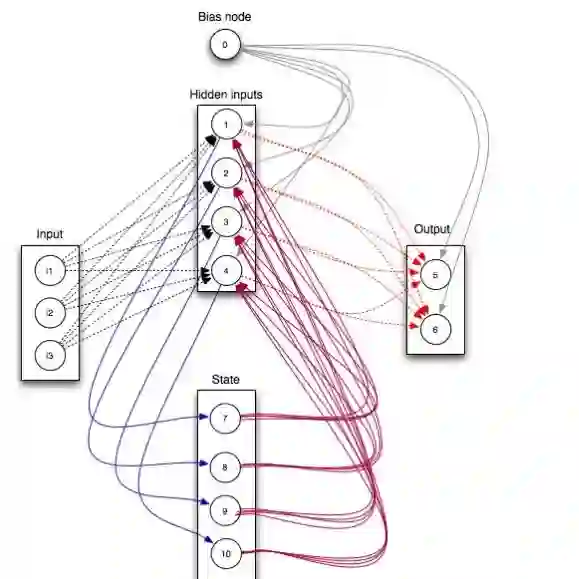
Training Restricted Boltzmann Machines (RBMs) has been challenging for a long time due to the difficulty of computing precisely the log-likelihood gradient. Over the past decades, many works have proposed more or less successful training recipes but without studying the crucial quantity of the problem: the mixing time, i.e. the number of Monte Carlo iterations needed to sample new configurations from a model. In this work, we show that this mixing time plays a crucial role in the dynamics and stability of the trained model, and that RBMs operate in two well-defined regimes, namely equilibrium and out-of-equilibrium, depending on the interplay between this mixing time of the model and the number of steps, $k$, used to approximate the gradient. We further show empirically that this mixing time increases with the learning, which often implies a transition from one regime to another as soon as $k$ becomes smaller than this time. In particular, we show that using the popular $k$ (persistent) contrastive divergence approaches, with $k$ small, the dynamics of the learned model are extremely slow and often dominated by strong out-of-equilibrium effects. On the contrary, RBMs trained in equilibrium display faster dynamics, and a smooth convergence to dataset-like configurations during the sampling. Finally we discuss how to exploit in practice both regimes depending on the task one aims to fulfill: (i) short $k$ can be used to generate convincing samples in short learning times, (ii) large $k$ (or increasingly large) is needed to learn the correct equilibrium distribution of the RBM. Finally, the existence of these two operational regimes seems to be a general property of energy based models trained via likelihood maximization.