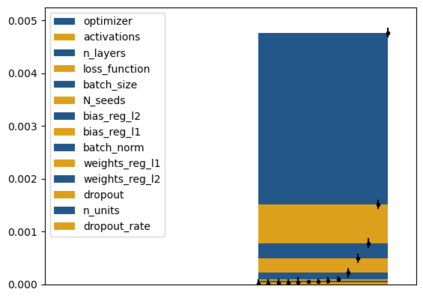
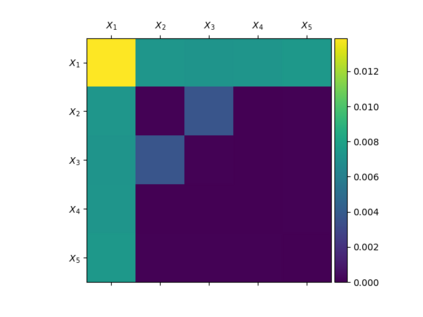
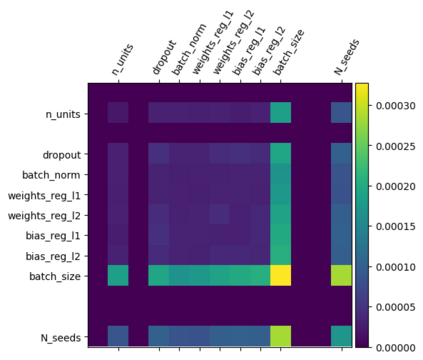
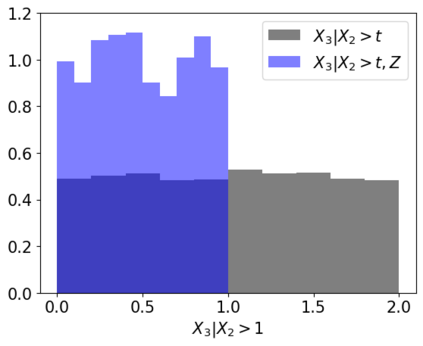
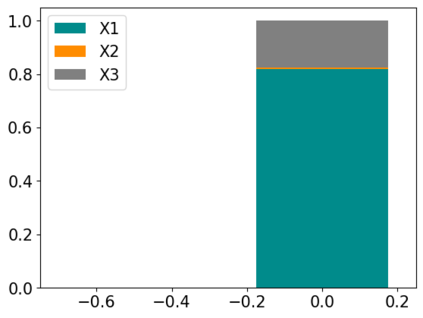
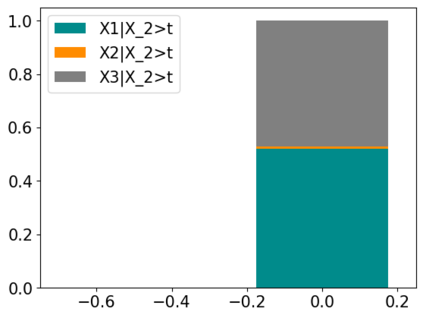
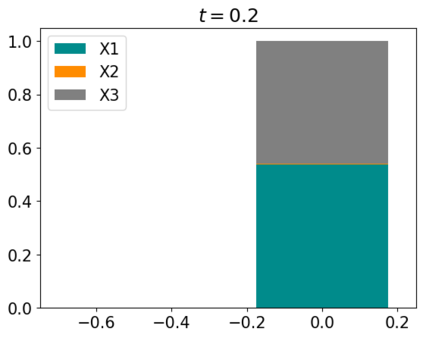
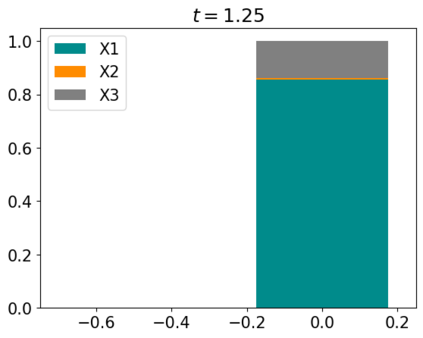
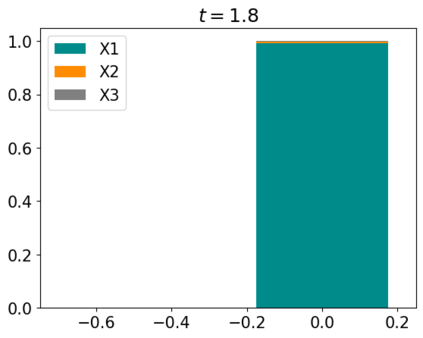
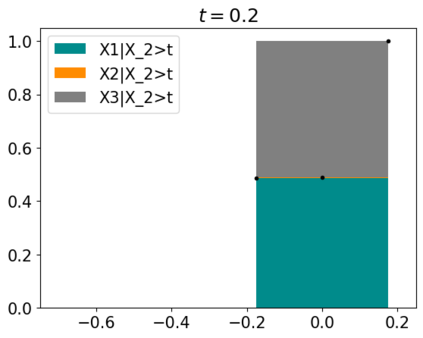
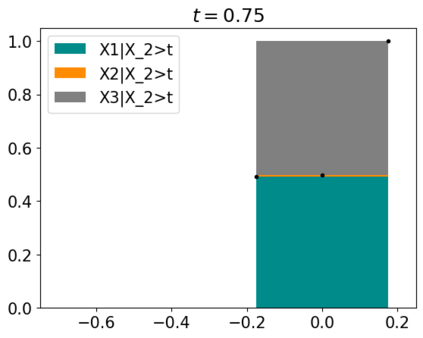
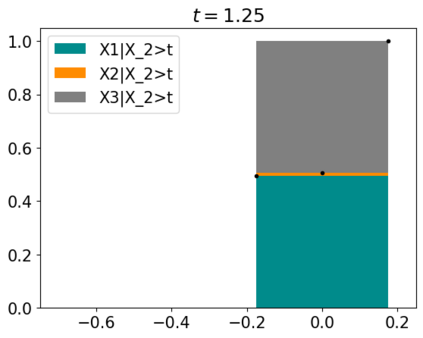
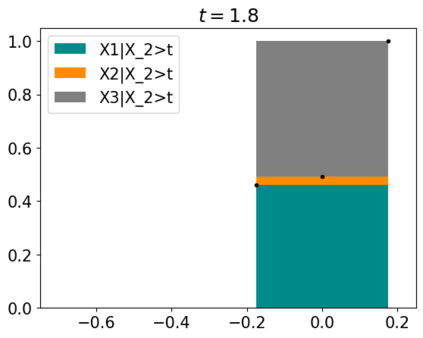
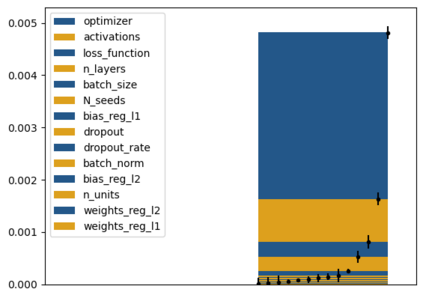
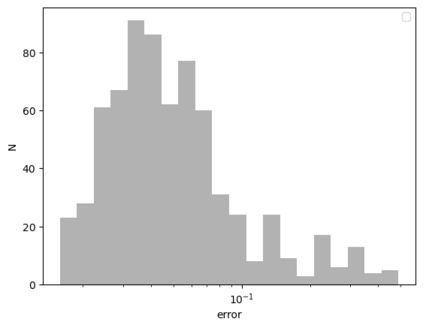
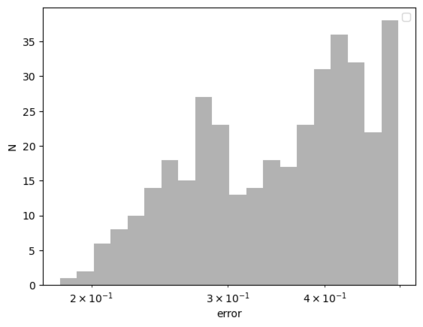
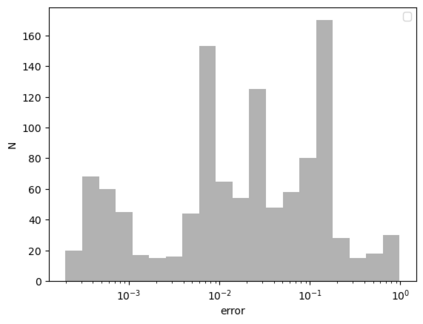
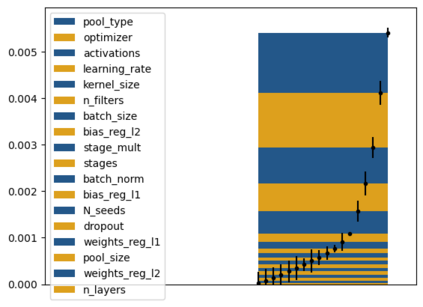
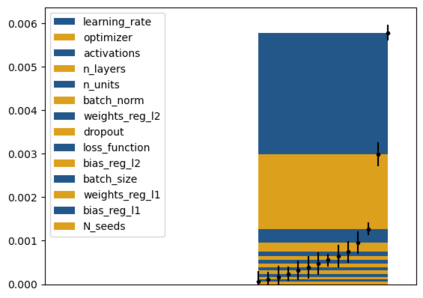
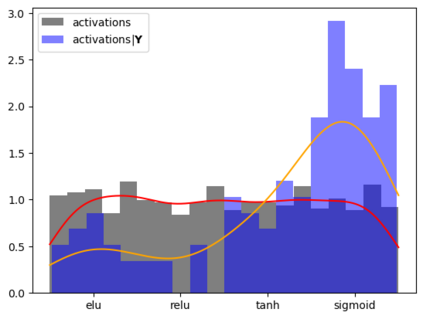
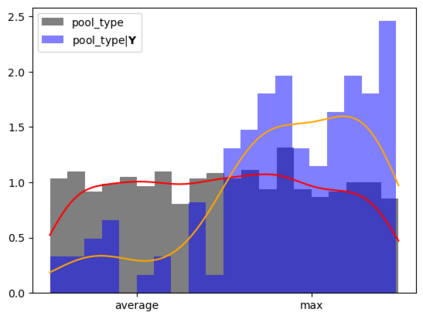
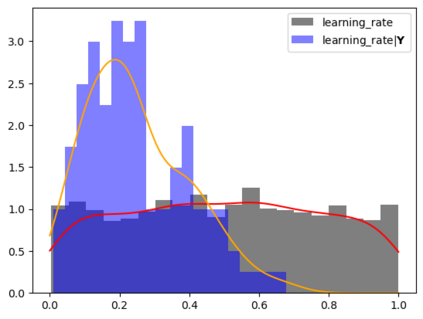
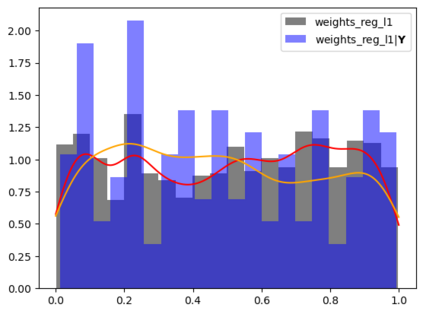
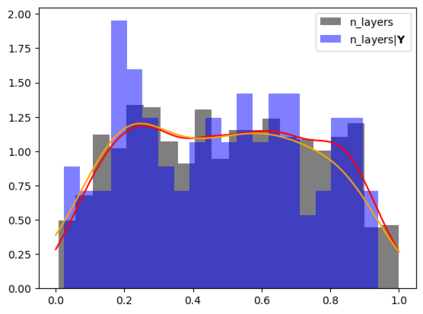
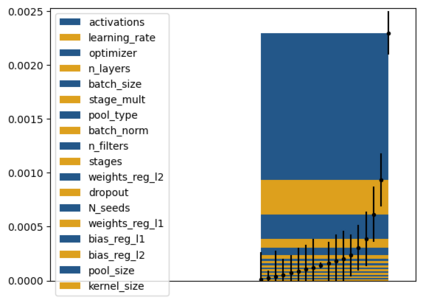
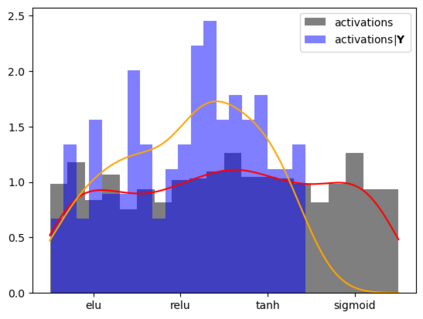
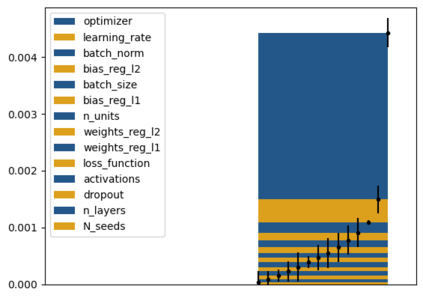
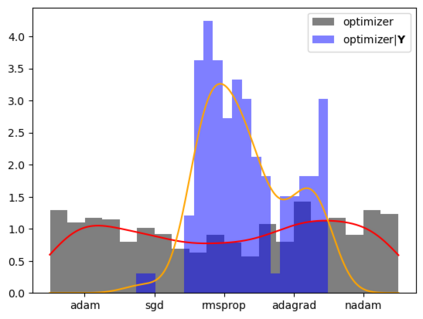
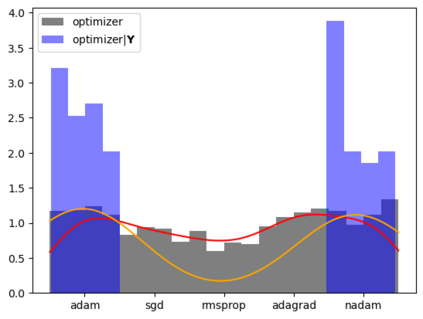
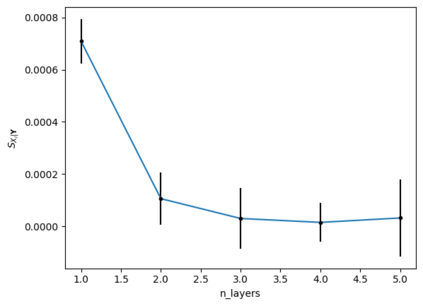
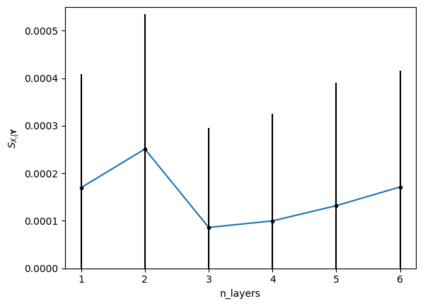
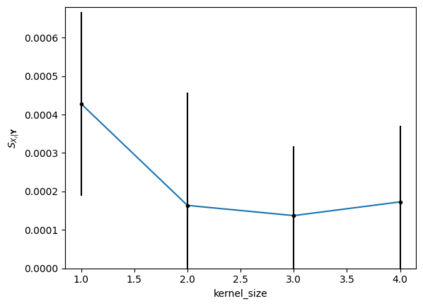
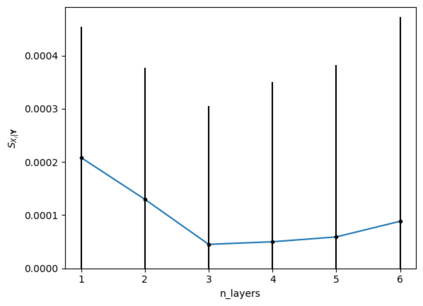
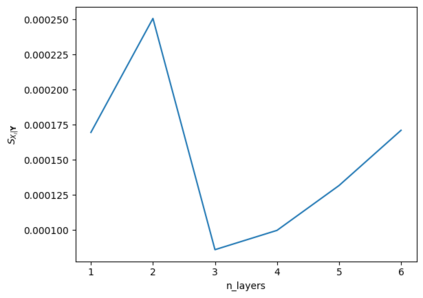
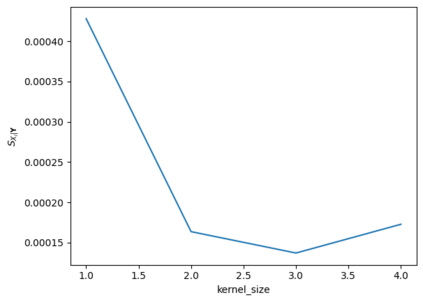
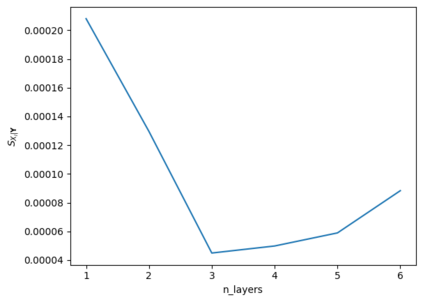
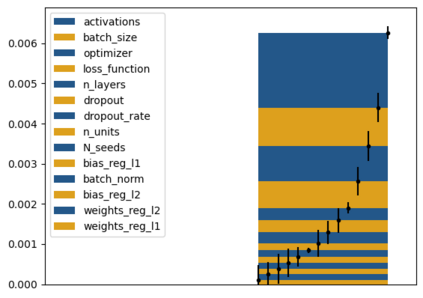
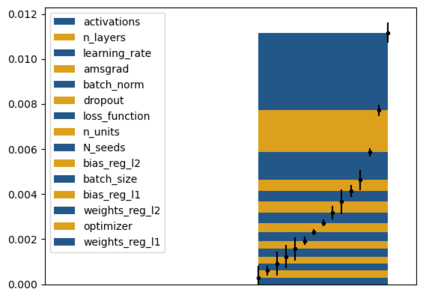
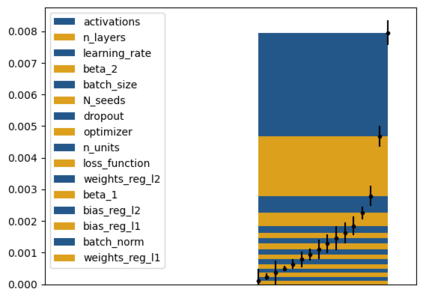
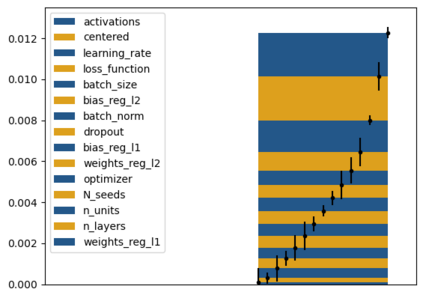
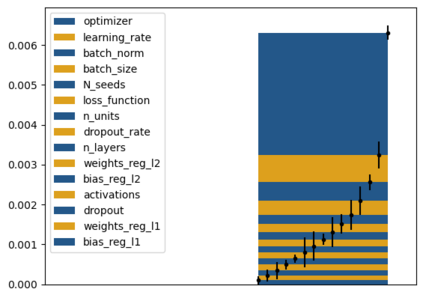
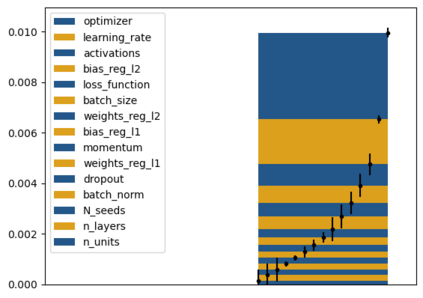
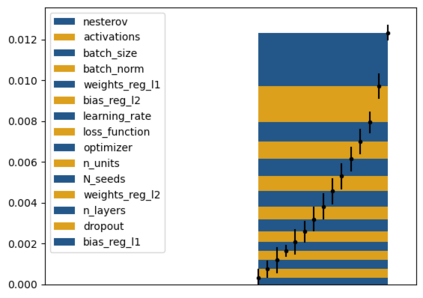
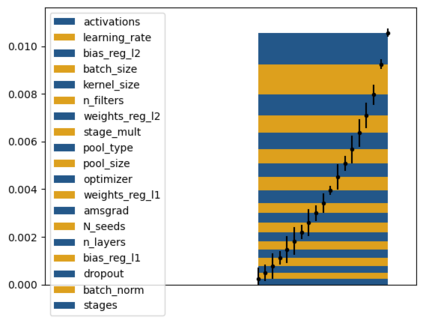
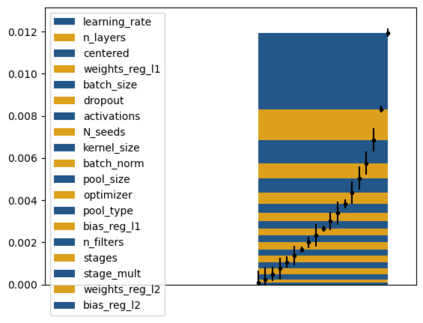
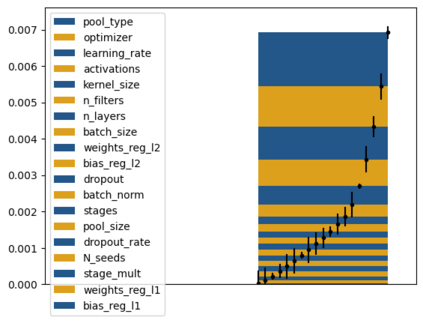
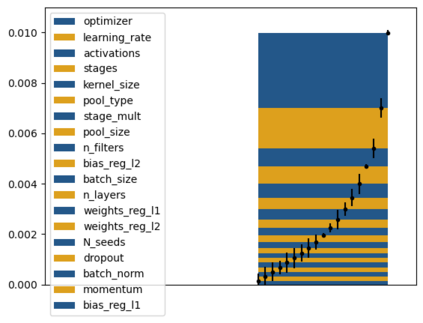
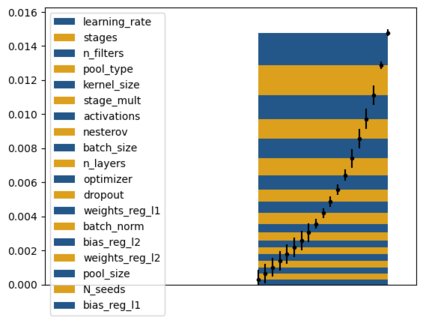
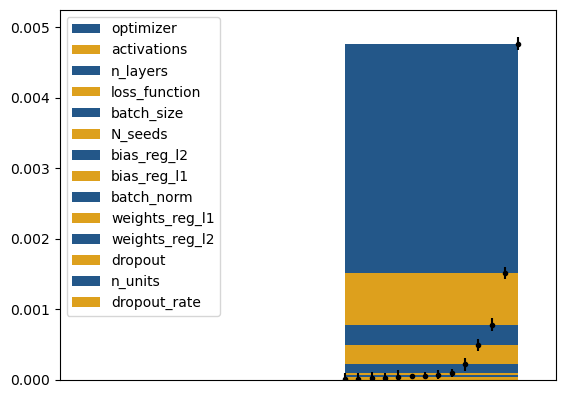
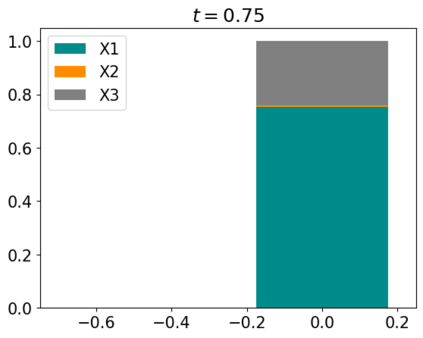Tackling new machine learning problems with neural networks always means optimizing numerous hyperparameters that define their structure and strongly impact their performances. In this work, we study the use of goal-oriented sensitivity analysis, based on the Hilbert-Schmidt Independence Criterion (HSIC), for hyperparameter analysis and optimization. Hyperparameters live in spaces that are often complex and awkward. They can be of different natures (categorical, discrete, boolean, continuous), interact, and have inter-dependencies. All this makes it non-trivial to perform classical sensitivity analysis. We alleviate these difficulties to obtain a robust analysis index that is able to quantify hyperparameters' relative impact on a neural network's final error. This valuable tool allows us to better understand hyperparameters and to make hyperparameter optimization more interpretable. We illustrate the benefits of this knowledge in the context of hyperparameter optimization and derive an HSIC-based optimization algorithm that we apply on MNIST and Cifar, classical machine learning data sets, but also on the approximation of Runge function and Bateman equations solution, of interest for scientific machine learning. This method yields neural networks that are both competitive and cost-effective.
翻译:处理神经网络中的新机器学习问题,总是意味着优化许多决定其结构并强烈影响其性能的超参数。在这项工作中,我们研究根据Hilbert-Schmidt独立标准(HSIC)进行的目标导向灵敏分析,以进行超参数分析和优化。超参数存在于往往复杂和尴尬的空格中。它们可以是不同性质(分类、离散、布林、连续)、相互作用和相互依存。所有这一切都使得进行典型敏感度分析非三重性。我们减轻了这些困难,以获得一个能够量化超参数对神经网络最后错误的相对影响的强力分析指数。这个宝贵的工具使我们能够更好地了解超参数,使超参数优化更易解释。我们说明了这种知识在超光度优化背景下的好处,并得出基于HSICSIC的优化算法,以及我们适用于MIT和Cifar、古典机器学习数据集的算法。我们也在运行函数和巴特曼方程式网络的近似匹配性影响上,这是高效的科学收益率方法。