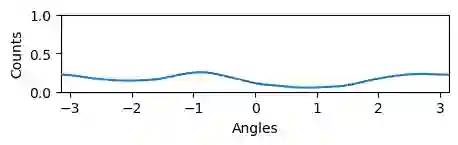
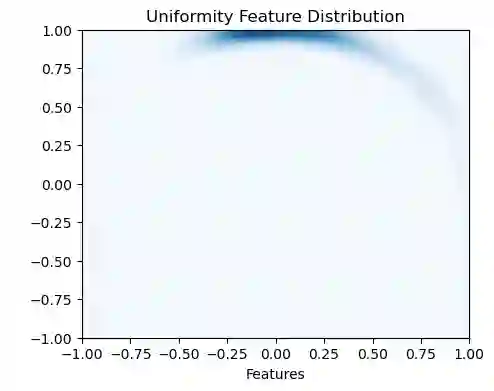
Bootstrap Your Own Latent (BYOL) introduced an approach to self-supervised learning avoiding the contrastive paradigm and subsequently removing the computational burden of negative sampling. However, feature representations under this paradigm are poorly distributed on the surface of the unit-hypersphere representation space compared to contrastive methods. This work empirically demonstrates that feature diversity enforced by contrastive losses is beneficial when employed in BYOL, and as such, provides greater inter-class feature separability. Therefore to achieve a more uniform distribution of features, we advocate the minimization of hyperspherical energy (i.e. maximization of entropy) in BYOL network weights. We show that directly optimizing a measure of uniformity alongside the standard loss, or regularizing the networks of the BYOL architecture to minimize the hyperspherical energy of neurons can produce more uniformly distributed and better performing representations for downstream tasks.
翻译:自我监督的学习方法避免了对比模式,并随后消除了负抽样的计算负担;然而,与对比方法相比,这一模式下的特征表现在单位-全屏代表空间表面分布不善,但与对比方法相比,在单位-全屏代表空间表面分布不善;这项工作从经验上表明,在BYOL雇用时,差异性损失造成的多样性是有益的,因此提供了更大的阶级间特征分离性。因此,为了实现特征的更统一分布,我们主张尽可能减少BYOL网络重量中的超球能(即最大限度地增加英特普)。我们表明,在标准损失的同时,直接优化统一度,或者使BYOL结构的网络正规化,以尽量减少神经元的超球性能量,可以产生更一致的分布,更好地表现下游任务。