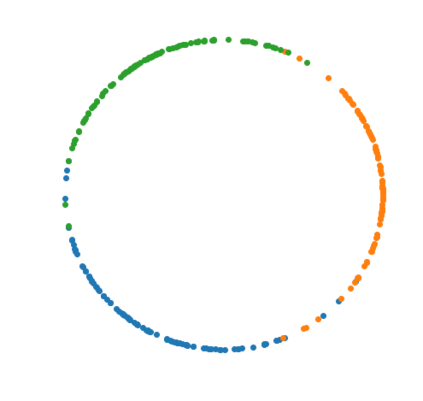
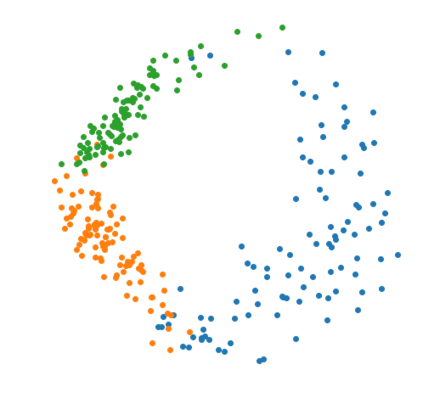
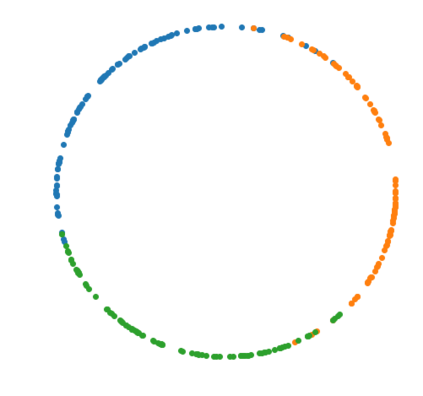
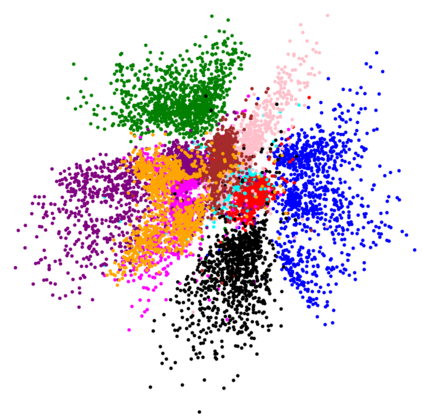
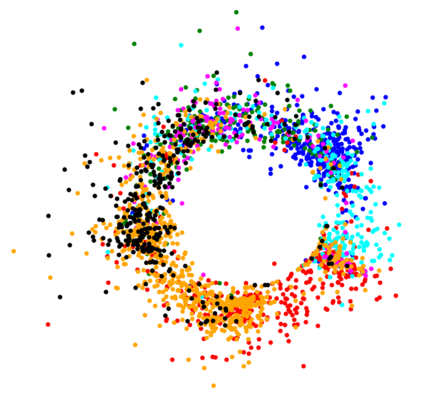
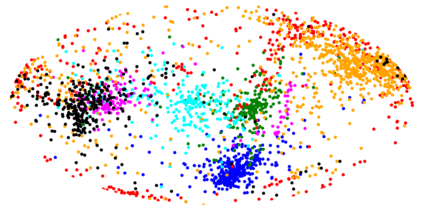
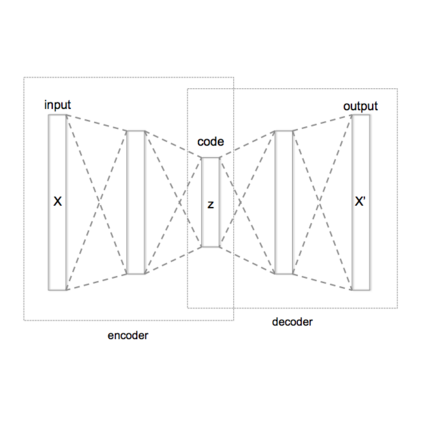
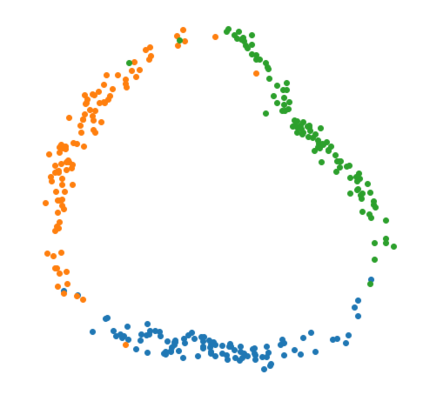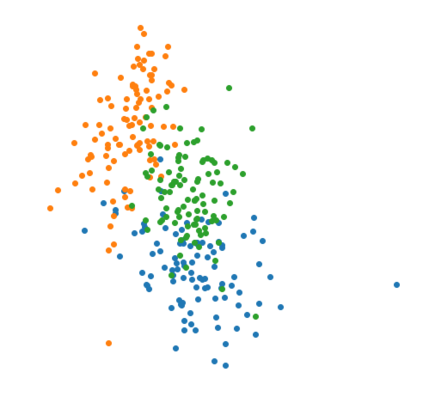The Variational Auto-Encoder (VAE) is one of the most used unsupervised machine learning models. But although the default choice of a Gaussian distribution for both the prior and posterior represents a mathematically convenient distribution often leading to competitive results, we show that this parameterization fails to model data with a latent hyperspherical structure. To address this issue we propose using a von Mises-Fisher (vMF) distribution instead, leading to a hyperspherical latent space. Through a series of experiments we show how such a hyperspherical VAE, or $\mathcal{S}$-VAE, is more suitable for capturing data with a hyperspherical latent structure, while outperforming a normal, $\mathcal{N}$-VAE, in low dimensions on other data types.
翻译:挥发自动编码器(VAE)是最常用的未受监督的机器学习模型之一。 但是,虽然默认地选择前一和后后二的高斯分布表示一种数学上方便的分布,常常导致竞争性结果,但我们显示,这个参数化无法用潜伏超球结构模拟数据。 为了解决这个问题,我们提议使用 von Mises-Fisher (VMF) 分布, 导致超球潜伏空间。 通过一系列实验, 我们展示了这样一个超球性VAE, 或$\mathcal{S}$-VAE, 如何更适合以超球性潜伏结构捕获数据, 而在其他数据类型上则比正常的$\mathcal{N}$VAE低维度运行。