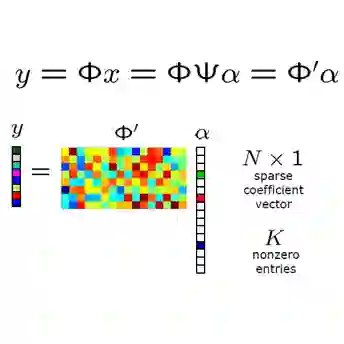
In order to determine the sparse approximation function which has a direct metric relationship with the $\ell_{0}$ quasi-norm, we introduce a wonderful triangle whose sides are composed of $\Vert \mathbf{x} \Vert_{0}$, $\Vert \mathbf{x} \Vert_{1}$ and $\Vert \mathbf{x} \Vert_{\infty}$ for any non-zero vector $\mathbf{x} \in \mathbb{R}^{n}$ by delving into the iterative soft-thresholding operator in this paper. Based on this triangle, we deduce the ratio $\ell_{1}$ and $\ell_{\infty}$ norms as a sparsity-promoting objective function for sparse signal reconstruction and also try to give the sparsity interval of the signal. Considering the $\ell_{1}/\ell_{\infty}$ minimization from a angle $\beta$ of the triangle corresponding to the side whose length is $\Vert \mathbf{x} \Vert_{\infty} - \Vert \mathbf{x} \Vert_{1}/\Vert \mathbf{x} \Vert_{0}$, we finally demonstrate the performance of existing $\ell_{1}/\ell_{\infty}$ algorithm by comparing it with $\ell_{1}/\ell_{2}$ algorithm.
翻译:暂无翻译