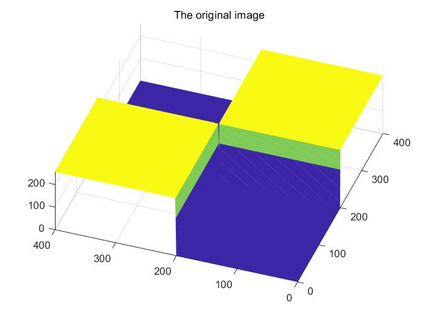
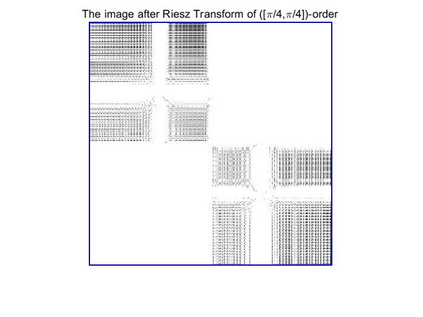
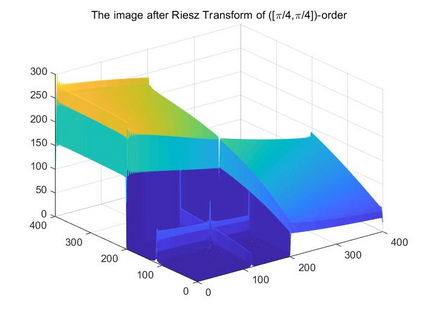
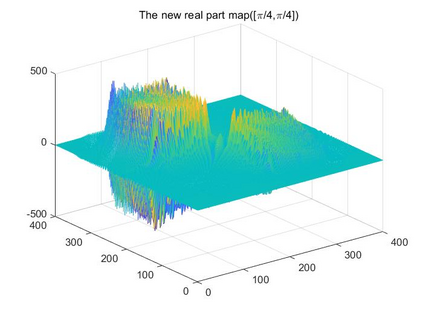
The fractional Hilbert transform was introduced by Zayed [30, Zayed, 1998] and has been widely used in signal processing. In view of is connection with the fractional Fourier transform, Chen, the first, second and fourth authors of this paper in [6, Chen et al., 2021] studied the fractional Hilbert transform and other fractional multiplier operators on the real line. The present paper is concerned with a natural extension of the fractional Hilbert transform to higher dimensions: this extension is the fractional Riesz transform which is defined by multiplication which a suitable chirp function on the fractional Fourier transform side. In addition to a thorough study of the fractional Riesz transforms, in this work we also investigate the boundedness of singular integral operators with chirp functions on rotation invariant spaces, chirp Hardy spaces and their relation to chirp BMO spaces, as well as applications of the theory of fractional multipliers in partial differential equations. Through numerical simulation, we provide physical and geometric interpretations of high-dimensional fractional multipliers. Finally, we present an application of the fractional Riesz transforms in edge detection which verifies a hypothesis insinuated in [26, Xu et al., 2016]. In fact our numerical implementation confirms that amplitude, phase, and direction information can be simultaneously extracted by controlling the order of the fractional Riesz transform.
翻译:Zayed [30, Zayed, 1998] 引入了分数Hilbert变换, 并在信号处理中被广泛使用。 鉴于与分数Freier变换有关, Chen, 本文在 [6, Chen et al., 2021] 中的第一、 第二和第四作者Chen在 [6, Chen, et al., 2021] 中研究了分数Hilbert变换和其他分数乘数操作员在真实线上的分数Hilbert变换, 以及分数Hilbert变换到更高维度的自然延伸: 此扩展是分数变换的分数Riesz变换, 由分数变换Fourier 变换的乘数函数来定义。 最后, 除了对分数变译Riesz变换的分数函数进行彻底研究之外, 我们还在这项工作中, 还调查了在变换数空间旋转、变数硬度硬度空间及其与 Chirp BMO 空间关系中应用分数乘数乘数变数理论的界限操作。 我们的分数变数变数变数变数变数Ries 和数变数变数变数级 级 级变数变数级 级 级 级