Fair Clustering Using Antidote Data

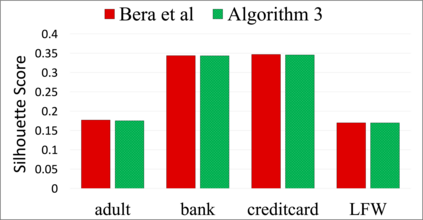
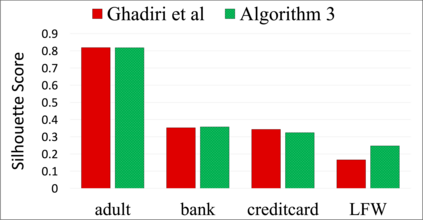
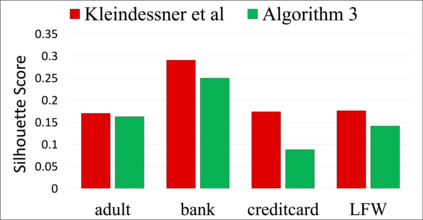
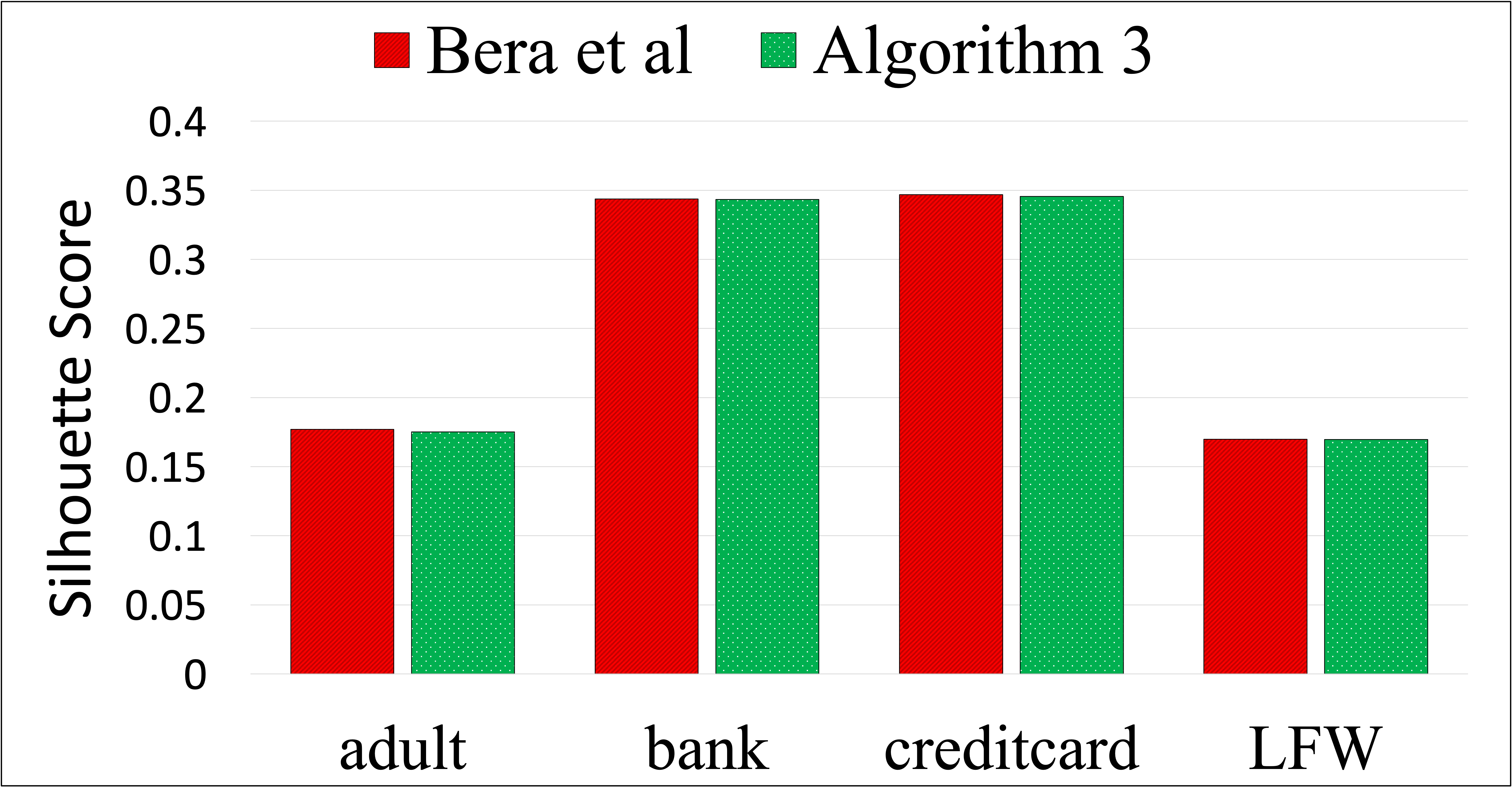
Clustering algorithms are widely utilized for many modern data science applications. This motivates the need to make outputs of clustering algorithms fair. Traditionally, new fair algorithmic variants to clustering algorithms are developed for specific notions of fairness. However, depending on the application context, different definitions of fairness might need to be employed. As a result, new algorithms and analysis need to be proposed for each combination of clustering algorithm and fairness definition. Additionally, each new algorithm would need to be reimplemented for deployment in a real-world system. Hence, we propose an alternate approach to fairness in clustering where we augment the original dataset with a small number of data points, called antidote data. When clustering is undertaken on this new dataset, the output is fair, for the chosen clustering algorithm and fairness definition. We formulate this as a general bi-level optimization problem which can accommodate any center-based clustering algorithms and fairness notions. We then categorize approaches for solving this bi-level optimization for different problem settings. Extensive experiments on different clustering algorithms and fairness notions show that our algorithms can achieve desired levels of fairness on many real-world datasets with a very small percentage of antidote data added. We also find that our algorithms achieve lower fairness costs and competitive clustering performance compared to other state-of-the-art fair clustering algorithms.