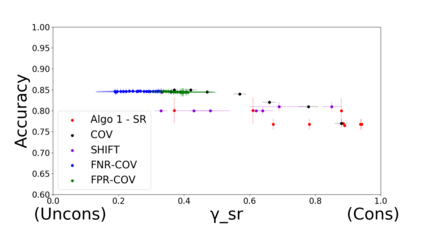
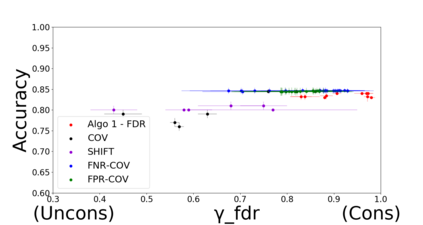
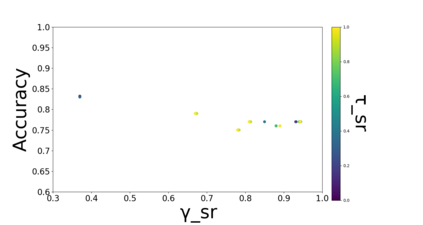
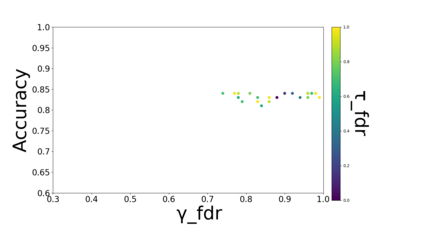
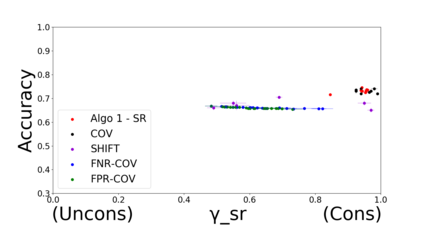
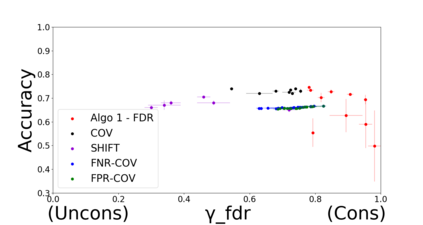
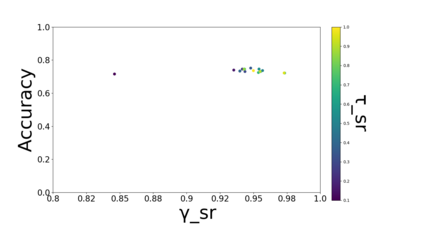
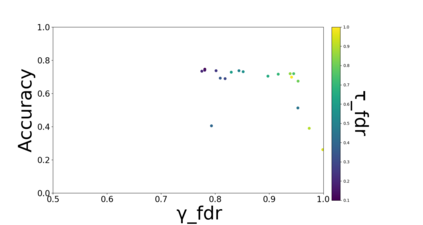
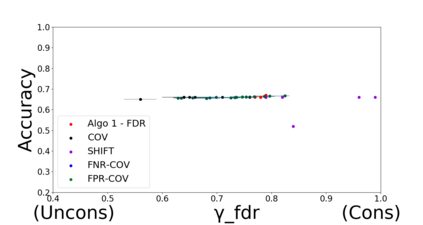
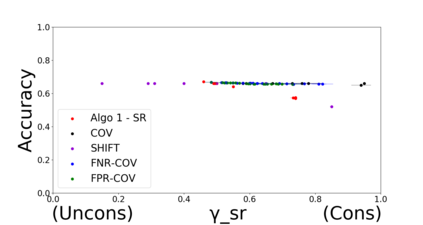
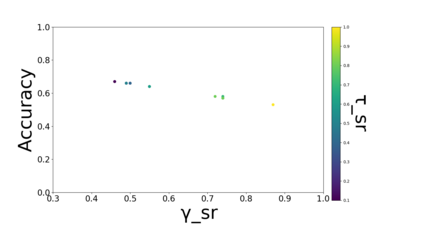
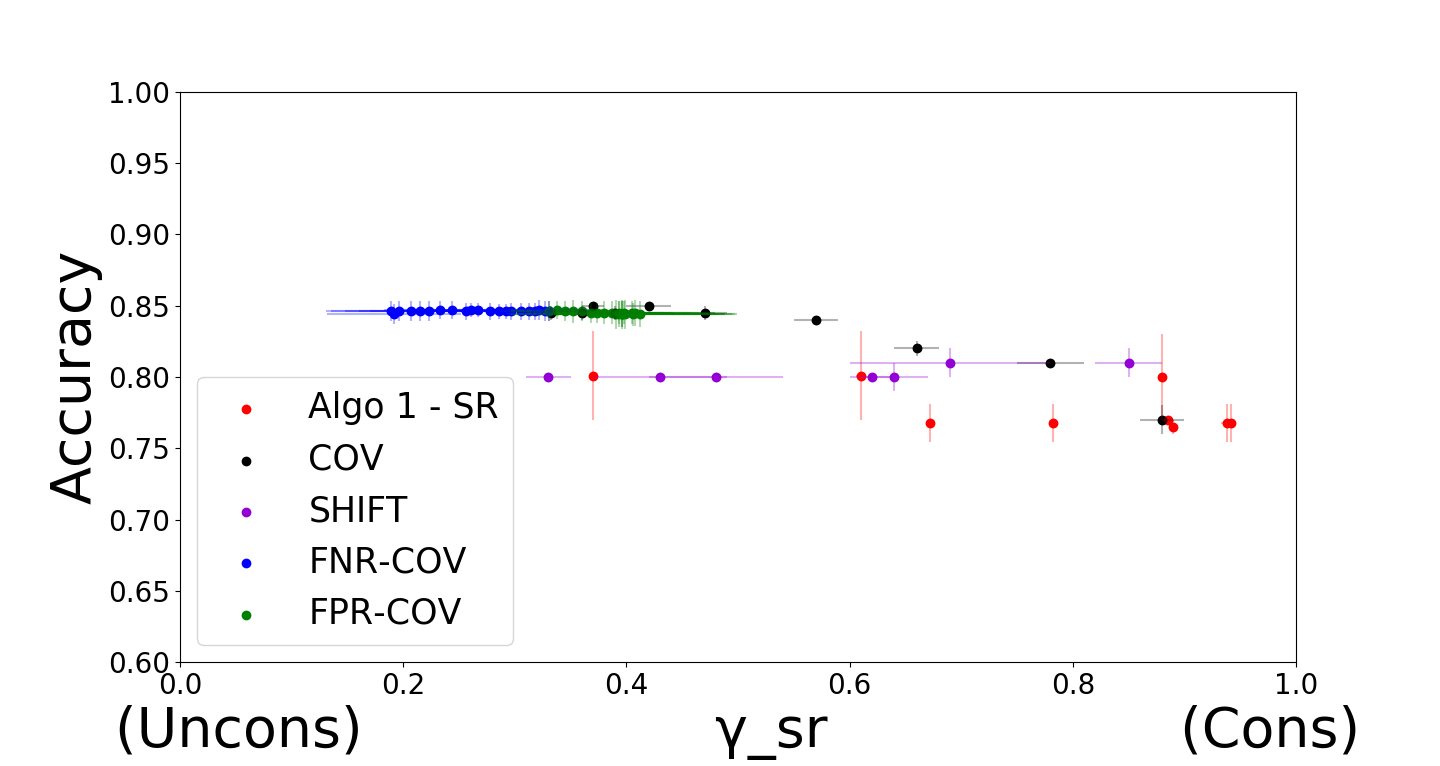
Developing classification algorithms that are fair with respect to sensitive attributes of the data has become an important problem due to the growing deployment of classification algorithms in various social contexts. Several recent works have focused on fairness with respect to a specific metric, modeled the corresponding fair classification problem as a constrained optimization problem, and developed tailored algorithms to solve them. Despite this, there still remain important metrics for which we do not have fair classifiers and many of the aforementioned algorithms do not come with theoretical guarantees; perhaps because the resulting optimization problem is non-convex. The main contribution of this paper is a new meta-algorithm for classification that takes as input a large class of fairness constraints, with respect to multiple non-disjoint sensitive attributes, and which comes with provable guarantees. This is achieved by first developing a meta-algorithm for a large family of classification problems with convex constraints, and then showing that classification problems with general types of fairness constraints can be reduced to those in this family. We present empirical results that show that our algorithm can achieve near-perfect fairness with respect to various fairness metrics, and that the loss in accuracy due to the imposed fairness constraints is often small. Overall, this work unifies several prior works on fair classification, presents a practical algorithm with theoretical guarantees, and can handle fairness metrics that were previously not possible.
翻译:由于在各种社会背景下越来越多地采用分类算法,因此,制定对数据敏感属性公平的分类算法已成为一个重要问题。最近的一些工作侧重于在特定指标方面的公平性,将相应的公平分类问题作为有限的优化问题模型,并开发了专门的算法来解决这些问题。尽管如此,仍然有一些重要的衡量法,我们没有公平的分类方法,许多上述算法也没有理论保障;或许因为由此产生的优化问题是非隐蔽的。本文的主要贡献是一个新的分类元值,它作为大量公平限制的投入,涉及多种非互不相容的敏感属性,并带有可辨的保证。这要通过首先为大量具有同系制约的分类问题大家庭的分类问题开发一个元值来实现,然后表明与一般类型的公平制约有关的分类问题可以减少到这个家庭。我们提出的实证结果表明,我们的算法在各种公平度衡量法方面可以实现近乎于完美的公平性,在多个非互不相容的敏感属性方面,并带有可辨证的保证。这要通过先验的准确性分析法的准确性,这往往会显示,因为先前的准确性的工作要求是公平性,而有可能使公平性分析方法的精确性限制。