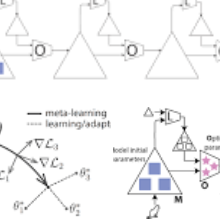
Meta-learning, or learning-to-learn, seeks to design algorithms that can utilize previous experience to rapidly learn new skills or adapt to new environments. Representation learning -- a key tool for performing meta-learning -- learns a data representation that can transfer knowledge across multiple tasks, which is essential in regimes where data is scarce. Despite a recent surge of interest in the practice of meta-learning, the theoretical underpinnings of meta-learning algorithms are lacking, especially in the context of learning transferable representations. In this paper, we focus on the problem of multi-task linear regression -- in which multiple linear regression models share a common, low-dimensional linear representation. Here, we provide provably fast, sample-efficient algorithms to address the dual challenges of (1) learning a common set of features from multiple, related tasks, and (2) transferring this knowledge to new, unseen tasks. Both are central to the general problem of meta-learning. Finally, we complement these results by providing information-theoretic lower bounds on the sample complexity of learning these linear features.
翻译:元学习,或学习到学习,试图设计能够利用以往经验迅速学习新技能或适应新环境的算法。代表性学习 -- -- 进行元学习的一个关键工具 -- -- 学习能够跨越多种任务转让知识的数据代表制,这是数据稀缺的制度所必不可少的。尽管最近人们对元学习实践的兴趣激增,但元学习算法的理论基础仍然缺乏,特别是在学习可转移的表述方面。在本文件中,我们侧重于多任务线性回归问题 -- -- 即多线性回归模型具有共同、低维度线性线性代表制。在这里,我们提供了可预见快速、高效的抽样算法,以应对以下双重挑战:(1) 从多重相关任务中学习一套共同特征,(2) 将这种知识转移到新的、看不见的任务。这两种知识都是元学习的一般性问题的核心。最后,我们通过提供有关学习这些线性特征的抽样复杂性的信息-理论较低界限来补充这些结果。