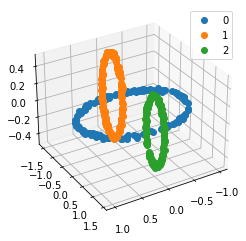
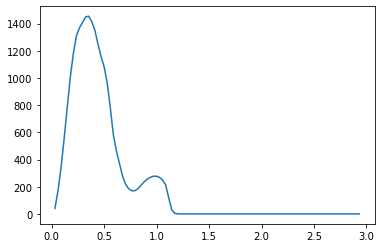
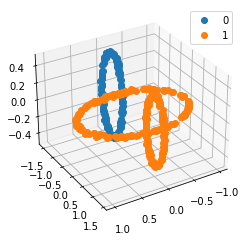
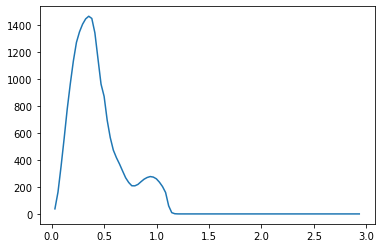
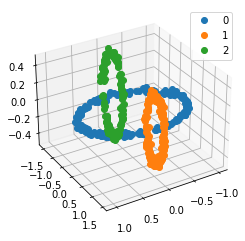
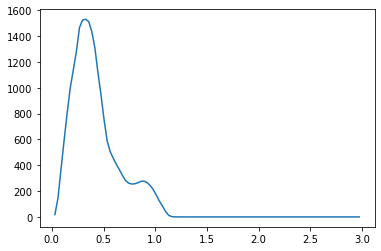
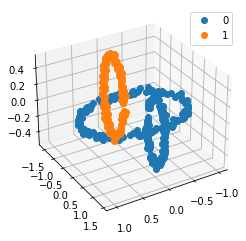
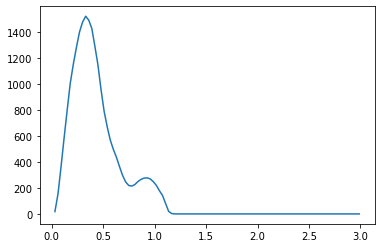
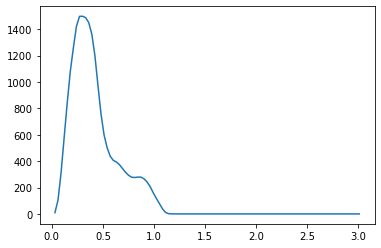
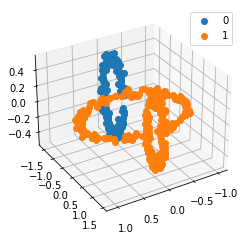
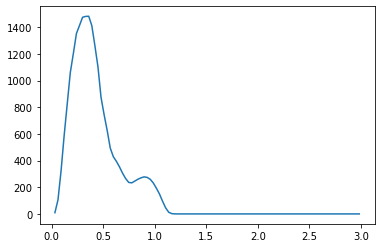
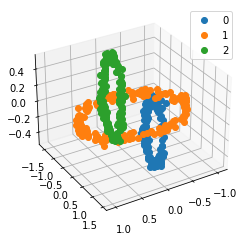
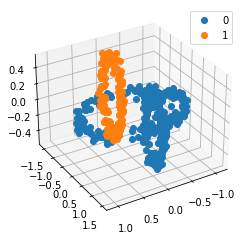
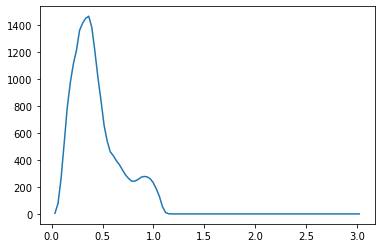
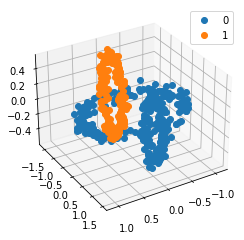
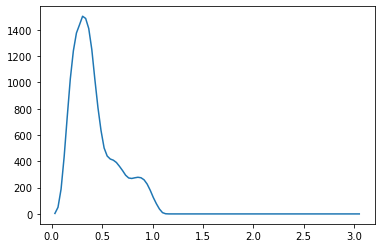
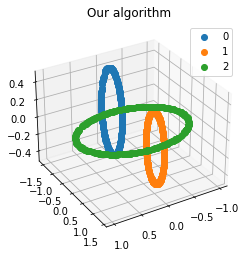
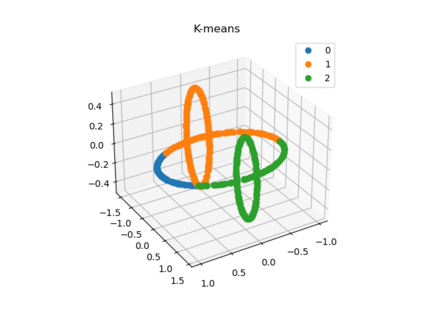
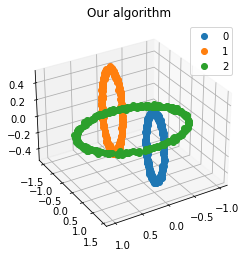
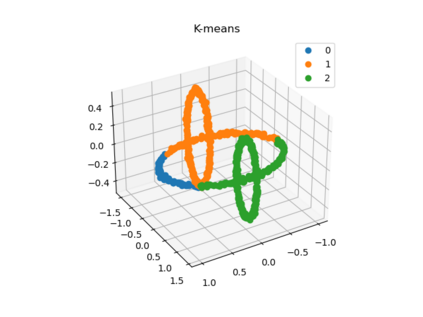
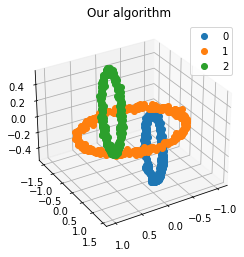
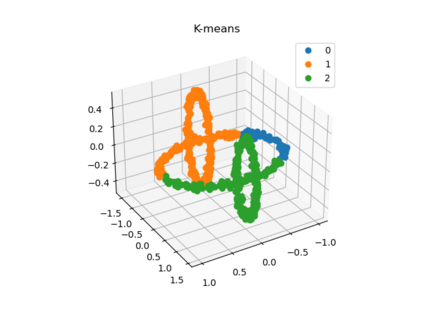
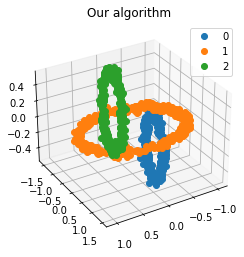
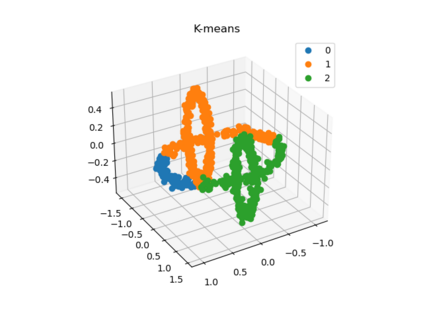
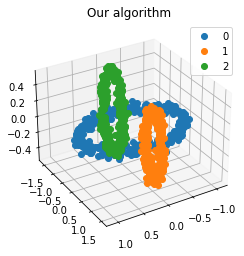
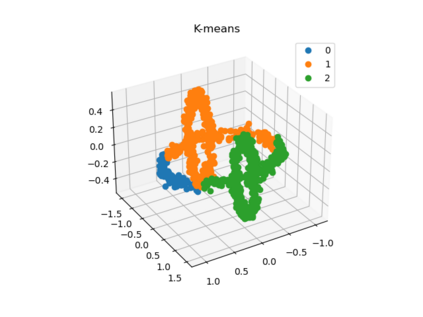
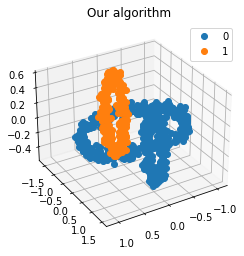
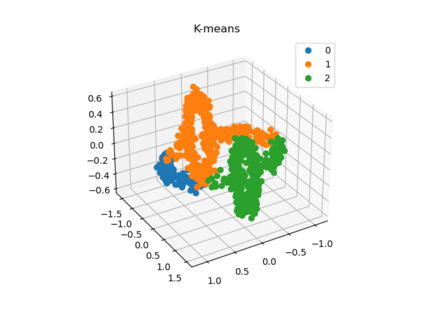
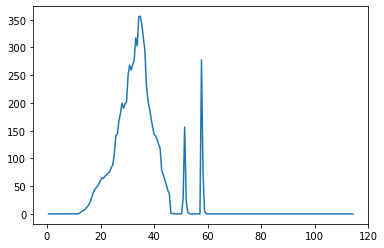
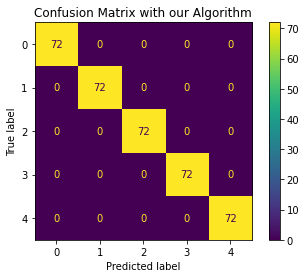
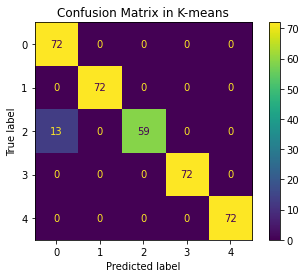
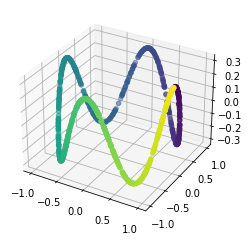
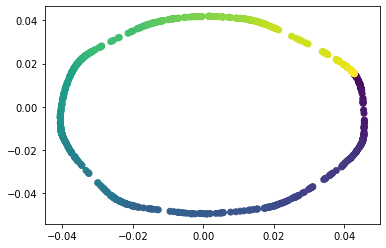
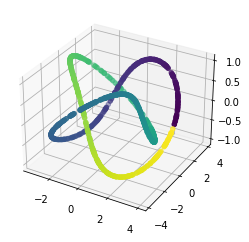
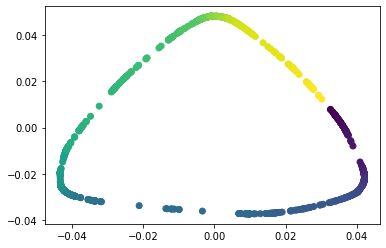
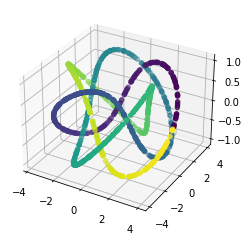
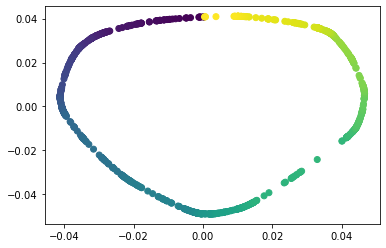
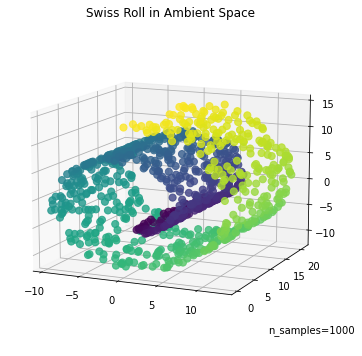
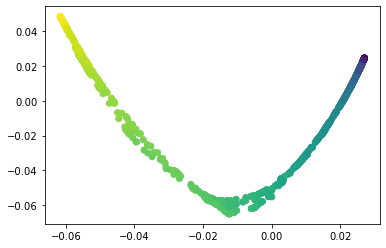
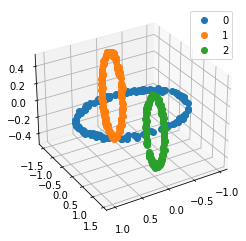
We propose a pair of completely data-driven algorithms for unsupervised classification and dimension reduction, and we empirically study their performance on a number of data sets, both simulated data in three-dimensions and images from the COIL-20 data set. The algorithms take as input a set of points sampled from a uniform distribution supported on a metric space, the latter embedded in an ambient metric space, and they output a clustering or reduction of dimension of the data. They work by constructing a natural family of graphs from the data and selecting the graph which maximizes the relative von Neumann entropy of certain normalized heat operators constructed from the graphs. Once the appropriate graph is selected, the eigenvectors of the graph Laplacian may be used to reduce the dimension of the data, and clusters in the data may be identified with the kernel of the associated graph Laplacian. Notably, these algorithms do not require information about the size of a neighborhood or the desired number of clusters as input, in contrast to popular algorithms such as $k$-means, and even more modern spectral methods such as Laplacian eigenmaps, among others. In our computational experiments, our clustering algorithm outperforms $k$-means clustering on data sets with non-trivial geometry and topology, in particular data whose clusters are not concentrated around a specific point, and our dimension reduction algorithm is shown to work well in several simple examples.
翻译:暂无翻译