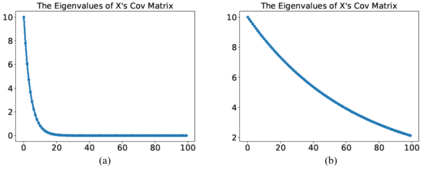
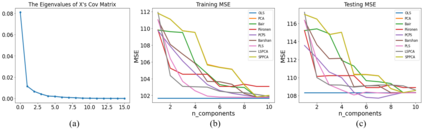
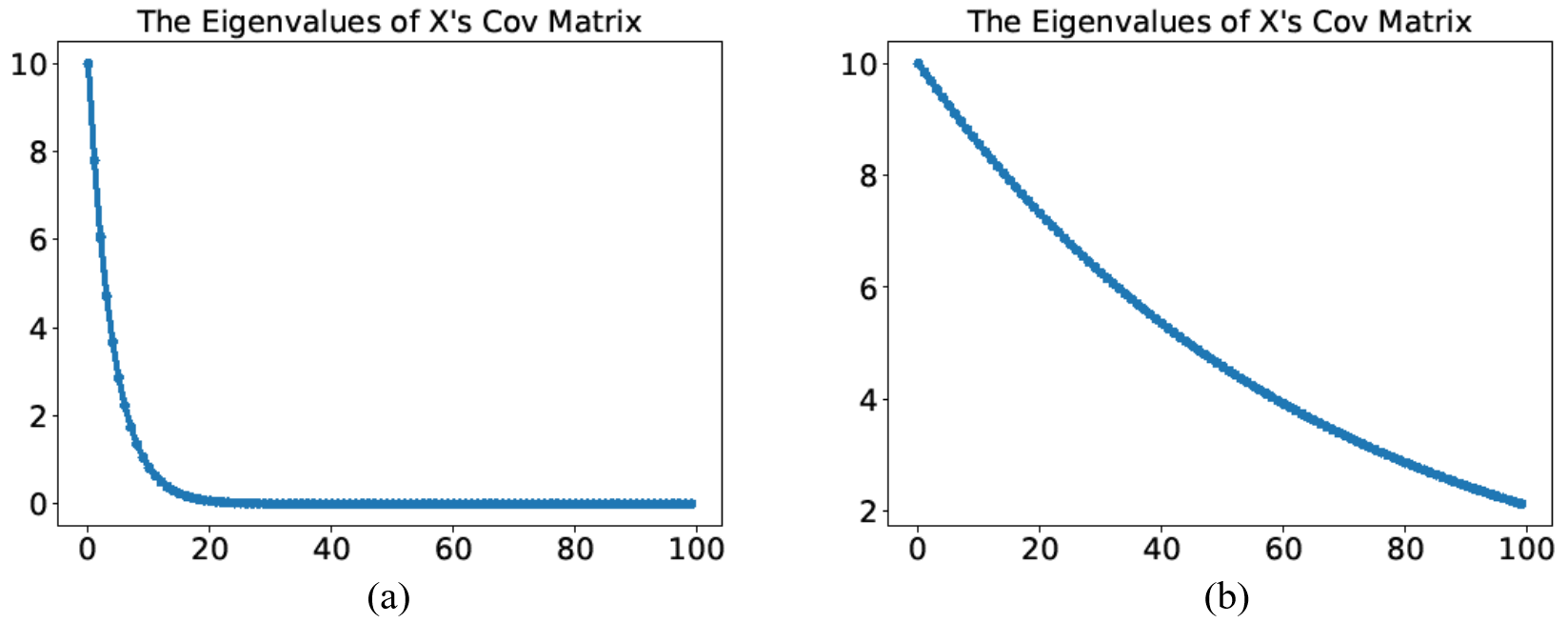
Principal component analysis (PCA) is a well-known linear dimension-reduction method that has been widely used in data analysis and modeling. It is an unsupervised learning technique that identifies a suitable linear subspace for the input variable that contains maximal variation and preserves as much information as possible. PCA has also been used in prediction models where the original, high-dimensional space of predictors is reduced to a smaller, more manageable, set before conducting regression analysis. However, this approach does not incorporate information in the response during the dimension-reduction stage and hence can have poor predictive performance. To address this concern, several supervised linear dimension-reduction techniques have been proposed in the literature. This paper reviews selected techniques, extends some of them, and compares their performance through simulations. Two of these techniques, partial least squares (PLS) and least-squares PCA (LSPCA), consistently outperform the others in this study.
翻译:主要元件分析(PCA)是一种众所周知的线性分层减少法,在数据分析和建模中广泛使用;这是一种未经监督的学习技术,为输入变量确定一个合适的线性子空间,其中含有最大变异并尽可能保存大量信息;在预测模型中也使用了五氯苯甲醚,其中最初的高维预测器空间缩小到较小、更易于管理,在进行回归分析之前设置;然而,这一方法没有将反应中的信息纳入分层减少阶段,因此预测性性能差;为解决这一关切,在文献中提出了几种受监督的线性分层减少技术;本文审查了选定的技术,扩展了其中一些技术,并通过模拟比较了这些技术的性能;其中两种技术,即部分最小平方和最小方的五氯苯甲醚(LSPCA),始终优于本研究中的其他技术。