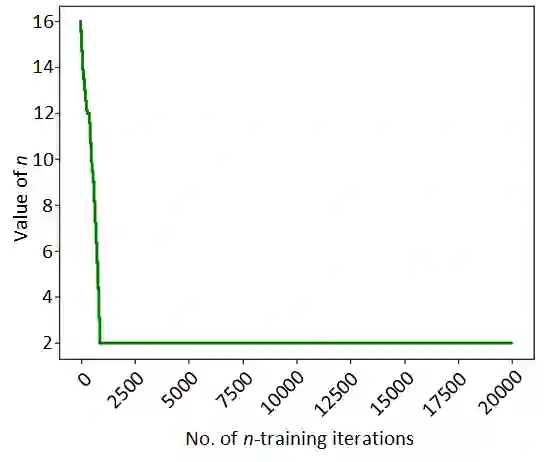
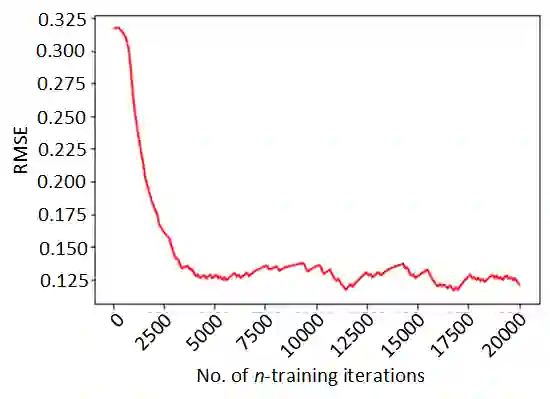
We consider the problem of finding the optimal value of n in the n-step temporal difference (TD) learning algorithm. We find the optimal n by resorting to a model-free optimization technique involving a one-simulation simultaneous perturbation stochastic approximation (SPSA) based procedure that we adopt to the discrete optimization setting by using a random projection approach. We prove the convergence of our proposed algorithm, SDPSA, using a differential inclusions approach and show that it finds the optimal value of n in n-step TD. Through experiments, we show that the optimal value of n is achieved with SDPSA for arbitrary initial values.
翻译:我们考虑如何在n步时间差分(TD)学习算法中找到最优的n值。我们采用基于一次仿真的同时扰动随机逼近(SPSA)技术来寻找最优n值,这是一种无模型优化技术,我们使用随机投影方法将其用于离散优化和搜索。我们采用微分包含法证明了我们提出的算法SDPSA的收敛性,并且展示了该算法可以在任意初始值下找到n步TD的最优n值。通过实验,我们证明了SDPSA可以实现最优n值的寻找。