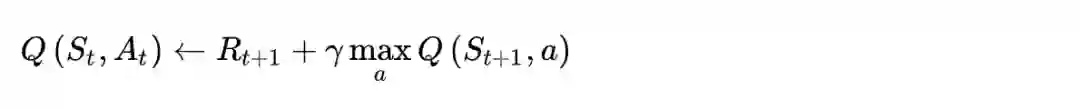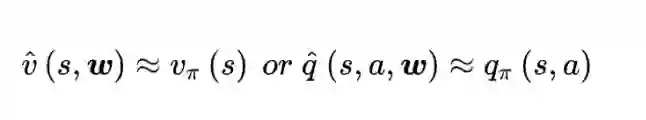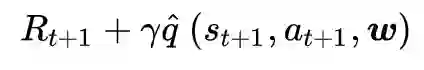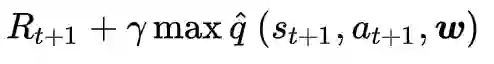强化学习扫盲贴：从Q-learning到DQN

2019 年 10 月 13 日 夕小瑶的卖萌屋

本文转载自知乎专栏「机器学习笔记」，原文作者「余帅」，链接
https://zhuanlan.zhihu.com/p/35882937

1 本文学习目标

1. 复习Q-Learning；
2. 理解什么是值函数近似（Function Approximation）；
3. 理解什么是DQN，弄清它和Q-Learning的区别是什么。

2 用Q-Learning解决经典迷宫问题

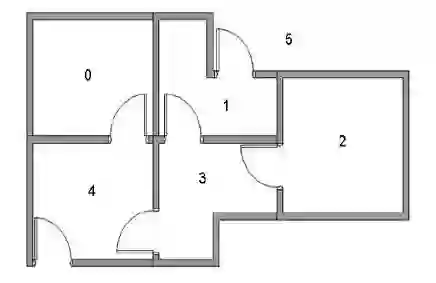
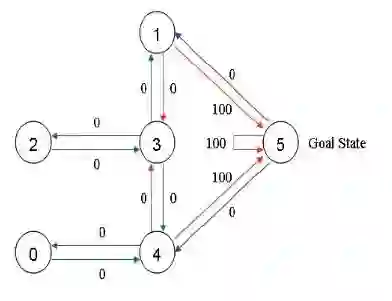
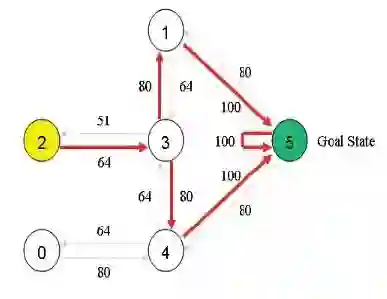
现有一个5房间的房子，如图1所示，房间与房间之间通过门连接，编号0到4,5号是房子外边，即我们的终点。我们将agent随机放在任一房间内，每打开一个房门返回一个reward。图2为房间之间的抽象关系图，箭头表示agent可以从该房间转移到与之相连的房间，箭头上的数字代表reward值。

图1 房子原型图

图2 抽象关系图

根据此关系，可以得到reward矩阵为

Q-Learning是一种off-policy TD方法，伪代码如图所示

Q-Learning伪代码

我们首先会初始化一个Q表，用于记录状态-动作对的值，每个episode中的每一步都会根据下列公式更新一次Q表

这里的迷宫问题，每一次episode的结束指的是到达终点状态5。为了简单起见，这里将学习率设为1，更新公式变为

另外，将衰减系数γ设为0.8。Q表初始化为一个5×5的全0矩阵。每次这样更新，最终Q表会收敛到一个矩阵。

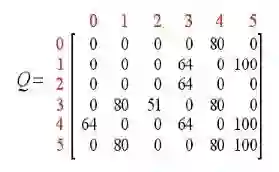
最终Q表收敛为

因此，也可以得到最优路径如下红色箭头所示

Python代码：

import numpy as np
GAMMA = 0.8
Q = np.zeros((6,6))
R=np.asarray([[-1,-1,-1,-1,0,-1],
   [-1,-1,-1,0,-1,100],
   [-1,-1,-1,0,-1,-1],
   [-1,0, 0, -1,0,-1],
   [0,-1,-1,0,-1,100],
   [-1,0,-1,-1,0,100]])
def getMaxQ(state):
    return max(Q[state, :])
def QLearning(state):
    curAction = None
    for action in range(6):
        if(R[state][action] == -1):
            Q[state, action]=0
        else:
            curAction = action
            Q[state,action]=R[state][action]+GAMMA * getMaxQ(curAction)
count=0
while count<1000:
    for i in range(6):
        QLearning(i)
    count+=1
print(Q/5)

Q-Learning方法很好的解决了这个迷宫问题，但是这终究只是一个小问题（状态空间和动作空间都很小），实际情况下，大部分问题都是有巨大的状态空间或者动作空间，想建立一个Q表，内存是绝对不允许的，而且数据量和时间开销也是个问题。

3 值函数近似与DQN

值函数近似（Function Approximation）的方法就是为了解决状态空间过大，也称为“维度灾难”的问题。通过用函数而不是Q表来表示，这个函数可以是线性的也可以使非线性的。

其中ω称为“权重”。那怎么把这个权重求出来，即拟合出这样一个合适的函数呢？这里就要结合机器学习算法里的一些有监督学习算法，对输入的状态提取特征作为输入，通过MC/TD计算出值函数作为输出，然后对函数参数 进行训练，直到收敛。这里主要说的是回归算法，比如线性回归、决策树、神经网络等。

这里，就可以引入DQN（Deep Q-Network）了，实际上它就是Q-Learning和神经网络的结合，将Q-Learning的Q表变成了Q-Network。

好，现在关键问题来了。这么去训练这个网络呢？换句话说，怎么去确定网络参ω呢？第一，我们需要一个Loss Function；第二，我们需要足够的训练样本。

训练样本好说，通过epsilon-greedy策略去生成就好。回忆一下Q-Learning，我们更新Q表是利用每步的reward和当前Q表来迭代的。那么我们可以用这个计算出来的Q值作为监督学习的“标签”来设计Loss Function，我们采用如下形式，即近似值和真实值的均方差

采用随机梯度下降法（SGD）来迭代求解，得到我们想要的，具体公式和过程还请看参考资料，这里不展开了，其实就是求导啦。值得一提的是，上述公式中的q(·)根据不同方法算出来，其形式不一样，比如利用MC，则为（回报）；利用TD(0)，则为

Q-Learning呢，就是

在David Silver的课里，他根据每次更新所参与样本量的不同把更新方法分为增量法（Incremental Methods）和批处理法（Batch Methods）。前者是来一个数据就更新一次，后者是先攒一堆样本，再从中采样一部分拿来更新Q网络，称之为“经验回放”，实际上DeepMind提出的DQN就是采用了经验回放的方法。为什么要采用经验回放的方法？因为对神经网络进行训练时，假设样本是独立同分布的。而通过强化学习采集到的数据之间存在着关联性，利用这些数据进行顺序训练，神经网络当然不稳定。经验回放可以打破数据间的关联。

最后附上DQN的伪代码

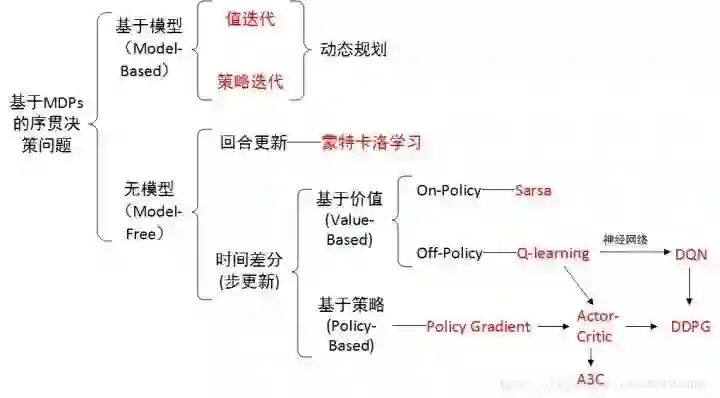
学到这里，其实可以做一个阶段性总结了，强化学习算法的基本框架可以用下图概括

参考文献

[1]Reinforcement Learning: An Introduction - Chapter 9: On-policy Prediction with Approximation
[2]Reinforcement Learning: An Introduction - Chapter 10: On-policy Control with Approximation
[3]David Silver’s RL Course Lecture 6 - Value Function Approximation (video, slides)
[4]DQN从入门到放弃5 深度解读DQN算法
[5]一条咸鱼的强化学习之路6之值函数近似（Value Function Approximation）和DQN

登录查看更多