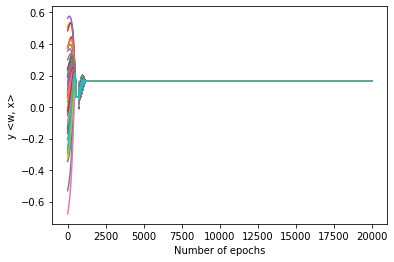
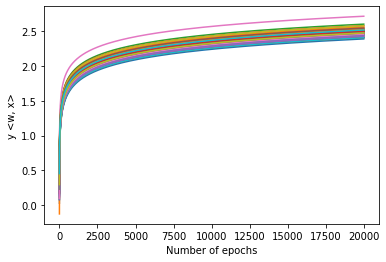
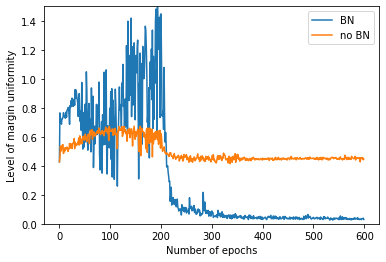
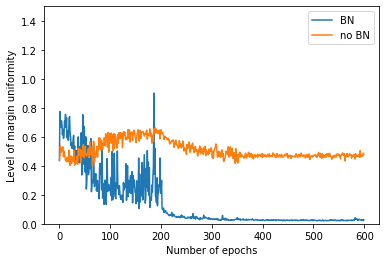
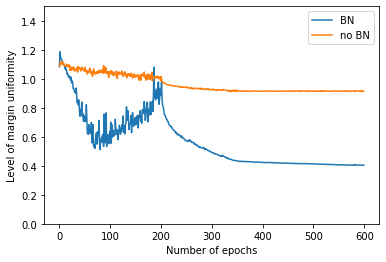
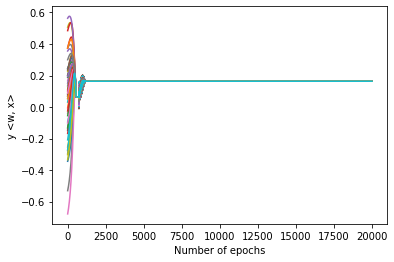
We study the implicit bias of batch normalization trained by gradient descent. We show that when learning a linear model with batch normalization for binary classification, gradient descent converges to a uniform margin classifier on the training data with an $\exp(-\Omega(\log^2 t))$ convergence rate. This distinguishes linear models with batch normalization from those without batch normalization in terms of both the type of implicit bias and the convergence rate. We further extend our result to a class of two-layer, single-filter linear convolutional neural networks, and show that batch normalization has an implicit bias towards a patch-wise uniform margin. Based on two examples, we demonstrate that patch-wise uniform margin classifiers can outperform the maximum margin classifiers in certain learning problems. Our results contribute to a better theoretical understanding of batch normalization.
翻译:暂无翻译