Quantum Potential Games, Replicator Dynamics, and the Separability Problem

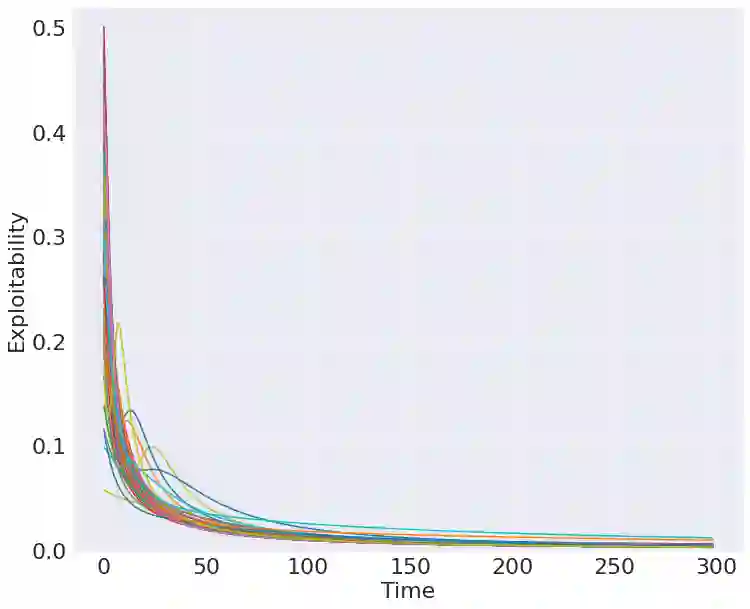
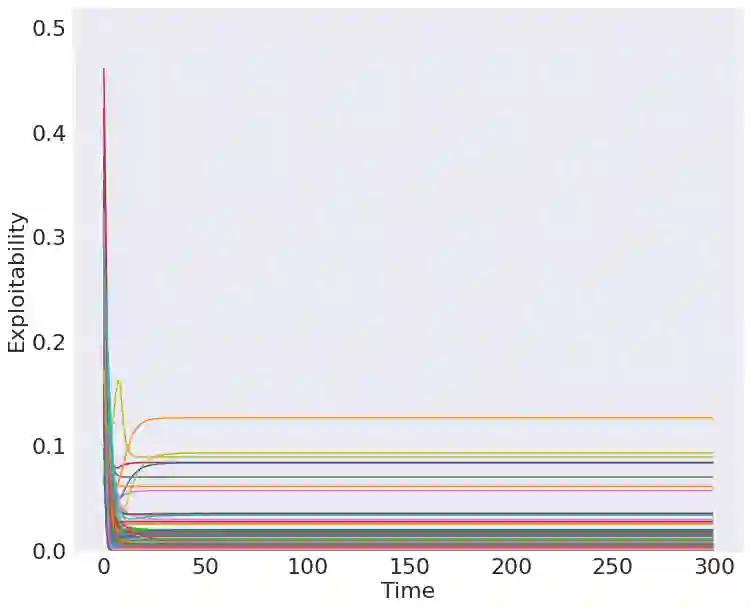
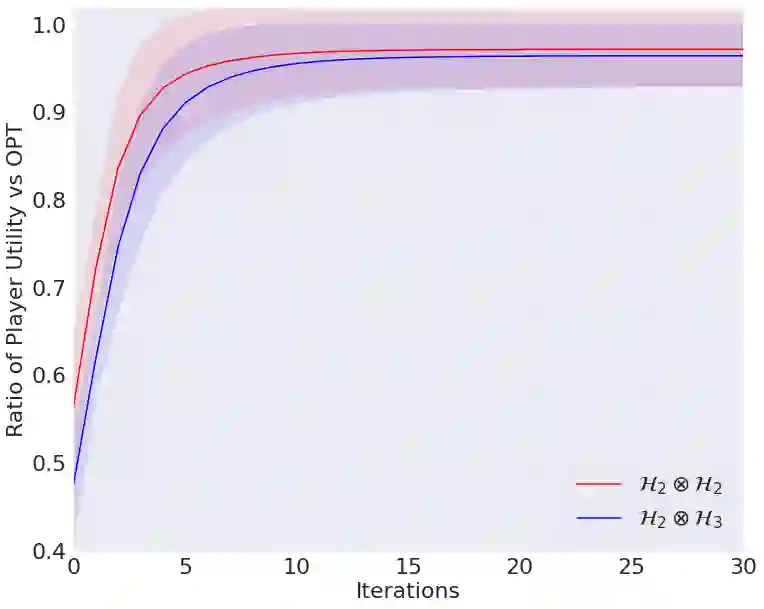
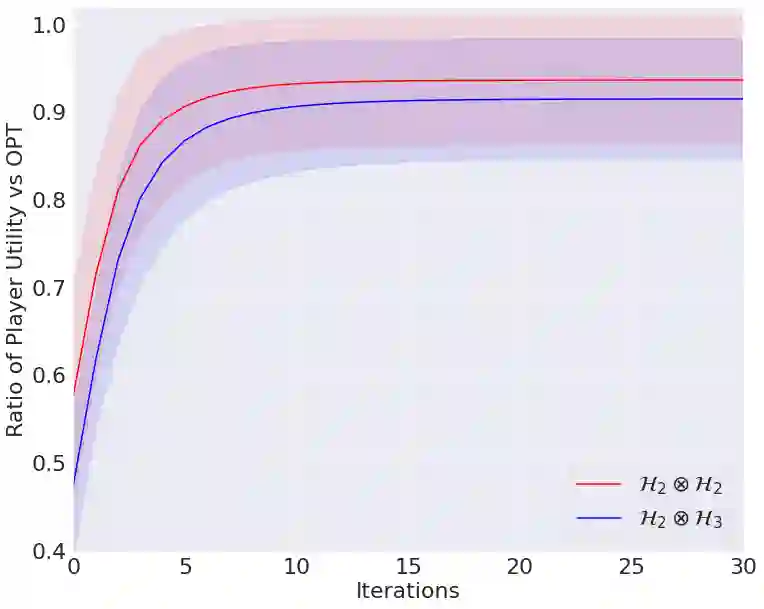
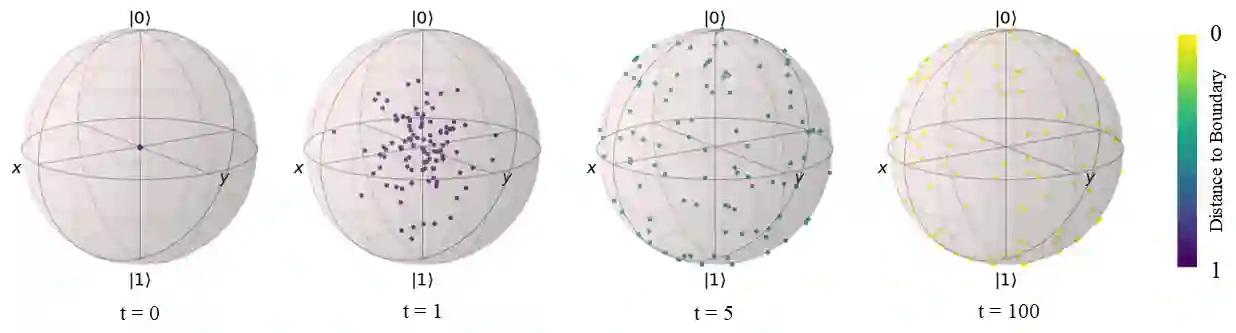
Learning in games has emerged as a powerful tool for Machine Learning with numerous applications. Several recent works have studied quantum zero-sum games, an extension of classical games where players have access to quantum resources, from a learning perspective. Going beyond the competitive regime, this work introduces quantum potential games as well as learning algorithms for this class of games. We introduce non-commutative extensions of the continuous-time replicator dynamics and the discrete-time Baum-Eagon/linear multiplicative weights update and study their convergence properties. Finally, we establish connections between quantum potential games and quantum separability, allowing us to reinterpret our learning dynamics as algorithms for the Best Separable State problem. We validate our theoretical findings through extensive experiments.