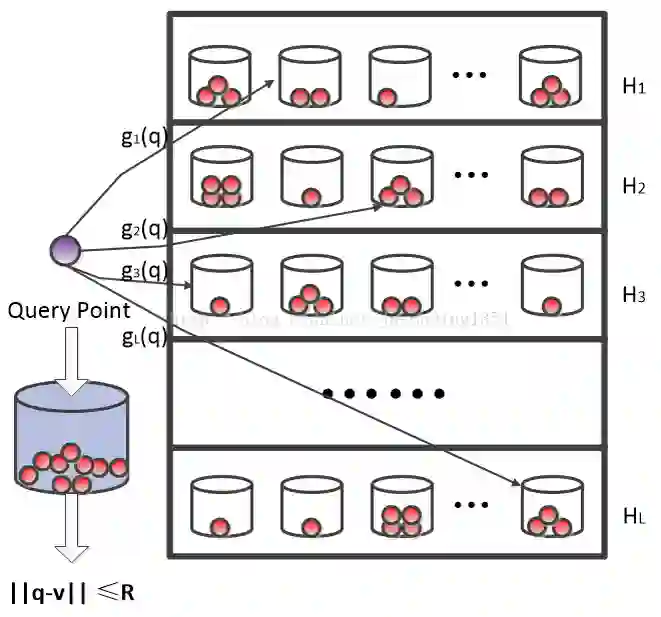
This work suggests faster and space-efficient index construction algorithms for LSH for Euclidean distance (\textit{a.k.a.}~\ELSH) and cosine similarity (\textit{a.k.a.}~\SRP). The index construction step of these LSHs relies on grouping data points into several bins of hash tables based on their hashcode. To generate an $m$-dimensional hashcode of the $d$-dimensional data point, these LSHs first project the data point onto a $d$-dimensional random Gaussian vector and then discretise the resulting inner product. The time and space complexity of both \ELSH~and \SRP~for computing an $m$-sized hashcode of a $d$-dimensional vector is $O(md)$, which becomes impractical for large values of $m$ and $d$. To overcome this problem, we propose two alternative LSH hashcode generation algorithms both for Euclidean distance and cosine similarity, namely, \CSELSH, \HCSELSH~and \CSSRP, \HCSSRP, respectively. \CSELSH~and \CSSRP~are based on count sketch \cite{count_sketch} and \HCSELSH~and \HCSSRP~utilize higher-order count sketch \cite{shi2019higher}. These proposals significantly reduce the hashcode computation time from $O(md)$ to $O(d)$. Additionally, both \CSELSH~and \CSSRP~reduce the space complexity from $O(md)$ to $O(d)$; ~and \HCSELSH, \HCSSRP~ reduce the space complexity from $O(md)$ to $O(N \sqrt[N]{d})$ respectively, where $N\geq 1$ denotes the size of the input/reshaped tensor. Our proposals are backed by strong mathematical guarantees, and we validate their performance through simulations on various real-world datasets.
翻译:暂无翻译