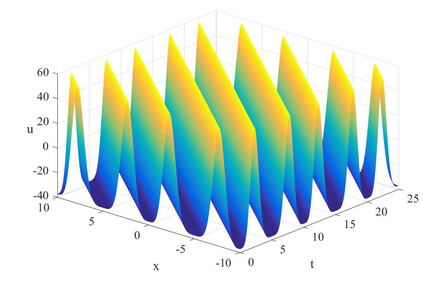
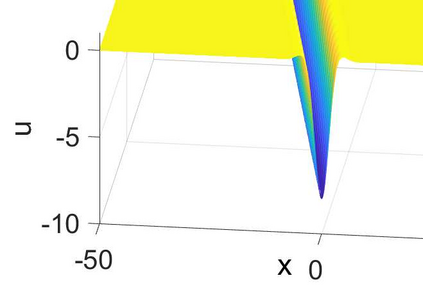
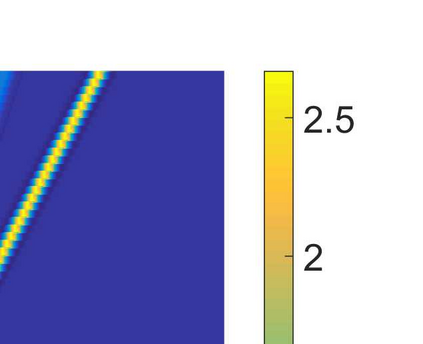
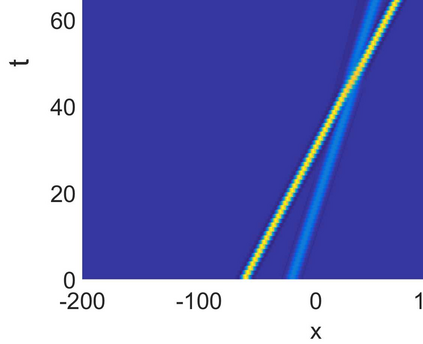
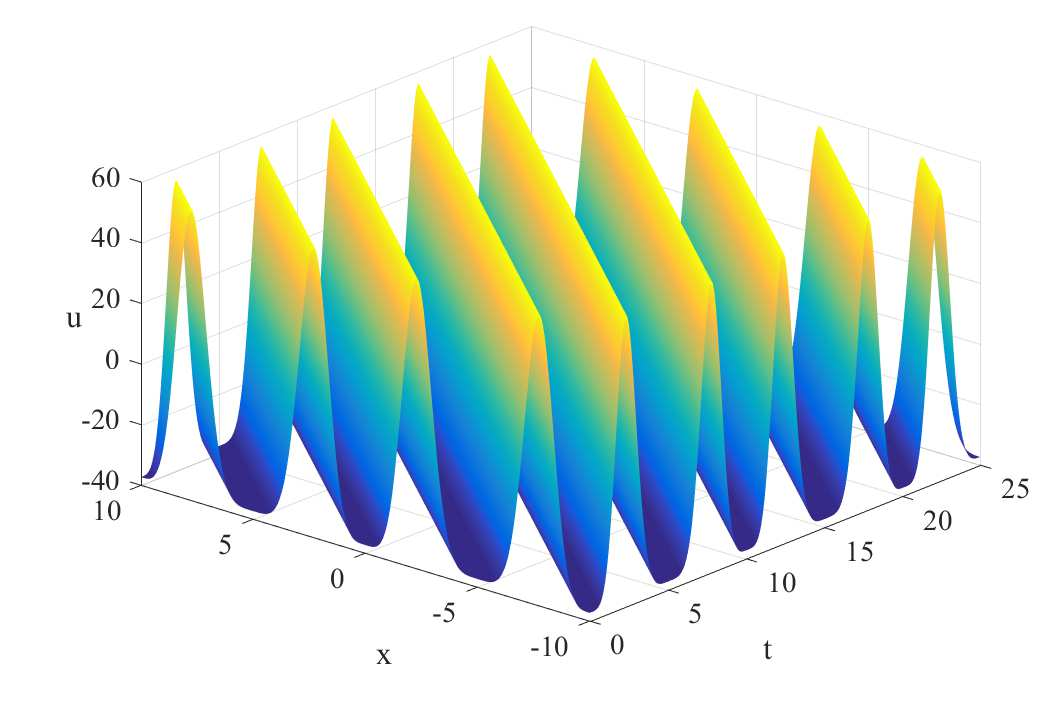
In this paper, we first consider the Rosenau equation with the quadratic nonlinearity and identify its Lie symmetry algebra. We obtain reductions of the equation to ODEs, and find periodic analytical solutions in terms of elliptic functions. Then, considering a general power-type nonlinearity, we prove the non-existence of solitary waves for some parameters using Pohozaev type identities. The Fourier pseudo-spectral method is proposed for the Rosenau equation with this single power type nonlinearity. In order to investigate the solitary wave dynamics, we generate the solitary wave profile as an initial condition by using the Petviashvili's method. Then the evolution of the single solitary wave and overtaking collision of solitary waves are investigated by various numerical experiments.
翻译:在本文中,我们首先考虑罗森瑙方程式的二次非线性,并找出它的利对称代数。我们从等式中削减了对数对数代数,并在椭圆函数方面找到定期的分析解决办法。然后,考虑到一般的电源型非线性,我们用Pohozaev 类型的身份来证明某些参数不存在单波。建议为罗森瑙方程采用Fourier伪光谱法,这种单电波非线性。为了调查单电波动态,我们使用Petviashvili 的方法将单波的进化和单波的过度碰撞作为初始条件。然后,通过各种数字实验来调查单波的演化和单波的过度碰撞。