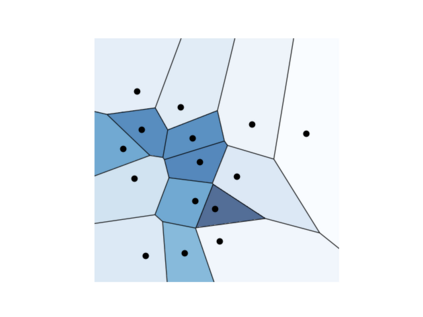
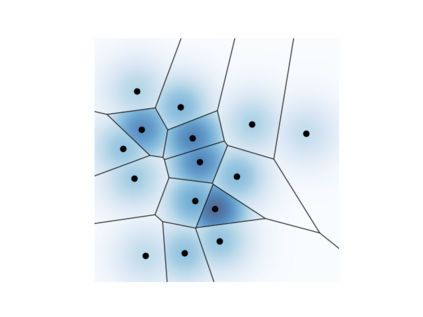
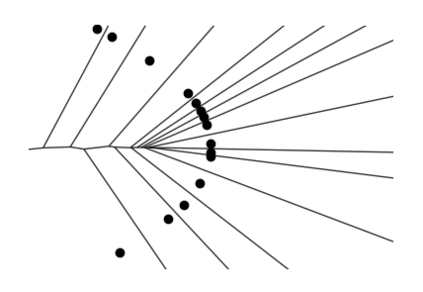
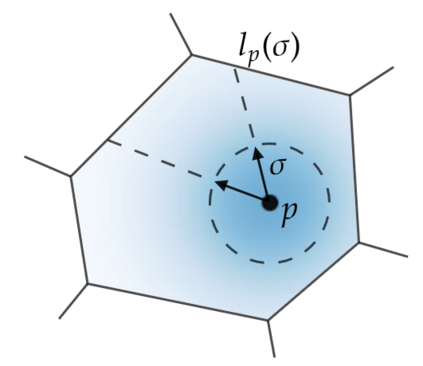
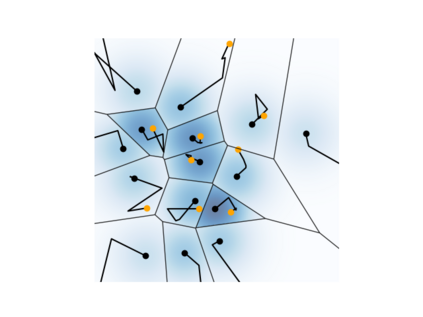
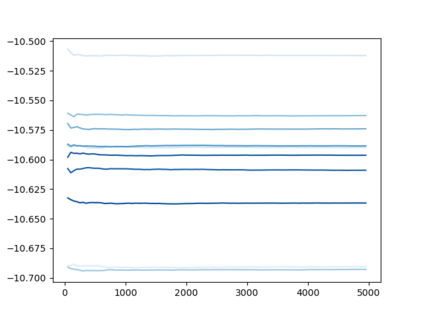
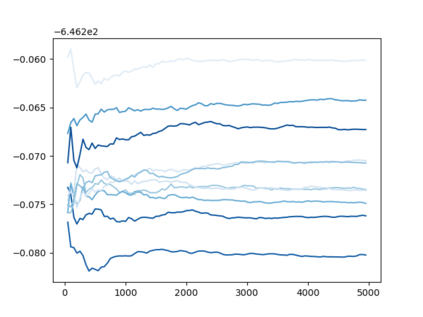
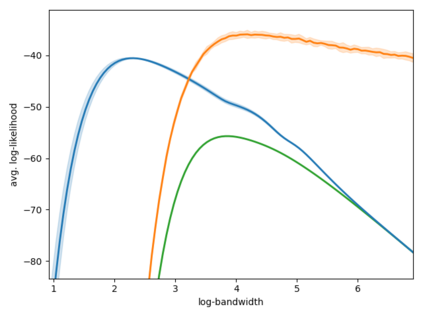
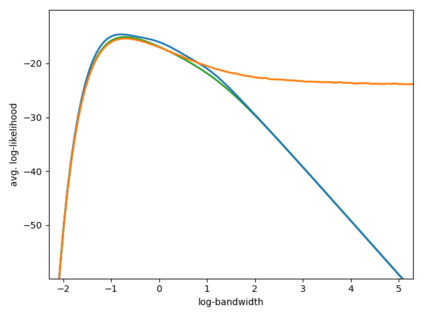
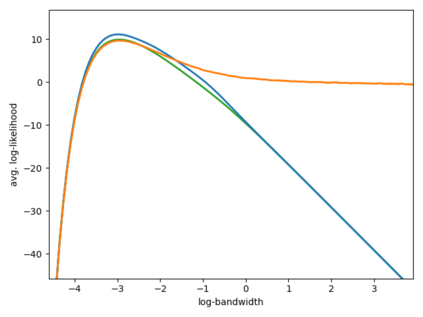
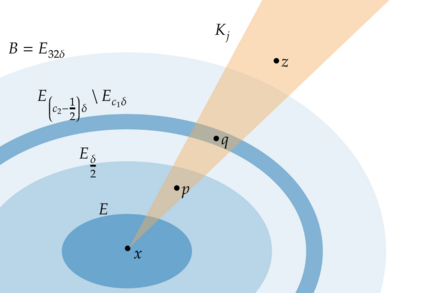
The Voronoi Density Estimator (VDE) is an established density estimation technique that adapts to the local geometry of data. However, its applicability has been so far limited to problems in two and three dimensions. This is because Voronoi cells rapidly increase in complexity as dimensions grow, making the necessary explicit computations infeasible. We define a variant of the VDE deemed Compactified Voronoi Density Estimator (CVDE), suitable for higher dimensions. We propose computationally efficient algorithms for numerical approximation of the CVDE and formally prove convergence of the estimated density to the original one. We implement and empirically validate the CVDE through a comparison with the Kernel Density Estimator (KDE). Our results indicate that the CVDE outperforms the KDE on sound and image data.
翻译:暂无翻译