A 4-Approximation Algorithm for Maximum Independent Set of Rectangles

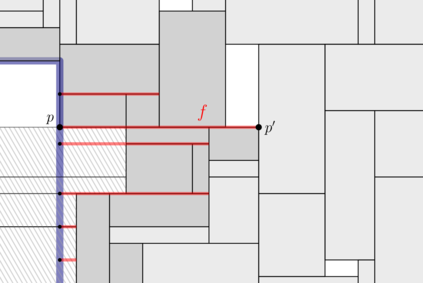
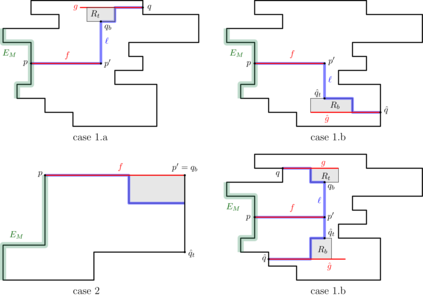
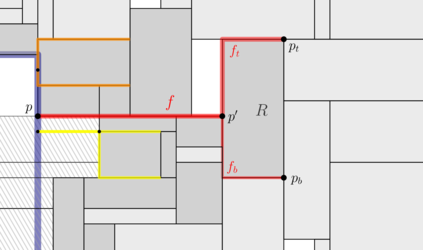
We study the Maximum Independent Set of Rectangles(MISR) problem, where we are given a set of axis-parallel rectangles in the plane and the goal is to select a subset of non-overlapping rectangles of maximum cardinality. In a recent breakthrough, Mitchell obtained the first constant-factor approximation algorithm for MISR. His algorithm achieves an approximation ratio of 10 and it is based on a dynamic program that intuitively recursively partitions the input plane into special polygons called corner-clipped rectangles (CCRs). In this paper, we present a 4-approximation algorithm for MISR which is based on a similar recursive partitioning scheme. However, we use a more general class of polygons -- polygons that are horizontally or vertically convex -- which allows us to provide an arguably simpler analysis and already improve the approximation ratio. Using a new fractional charging argument and fork-fences to guide the partitions, we improve the approximation ratio even more to 4. We hope that our ideas will lead to further progress towards a PTAS for MISR.