Approximation of SPDE covariance operators by finite elements: A semigroup approach

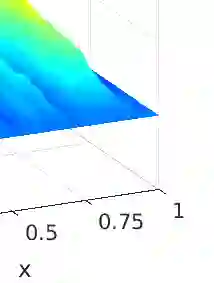
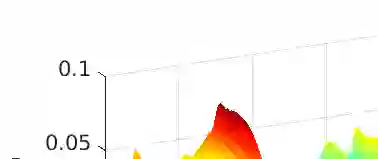
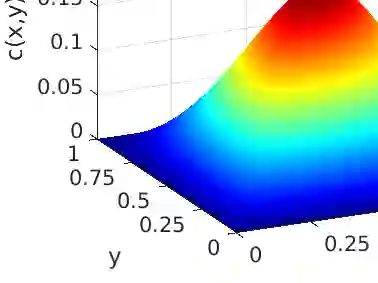
The problem of approximating the covariance operator of the mild solution to a linear stochastic partial differential equation is considered. An integral equation involving the semigroup of the mild solution is derived and a general error decomposition formula is proven. This formula is applied to approximations of the covariance operator of a stochastic advection-diffusion equation and a stochastic wave equation, both on bounded domains. The approximations are based on finite element discretizations in space and rational approximations of the exponential function in time. Convergence rates are derived in the trace class and Hilbert--Schmidt norms with numerical simulations illustrating the results.