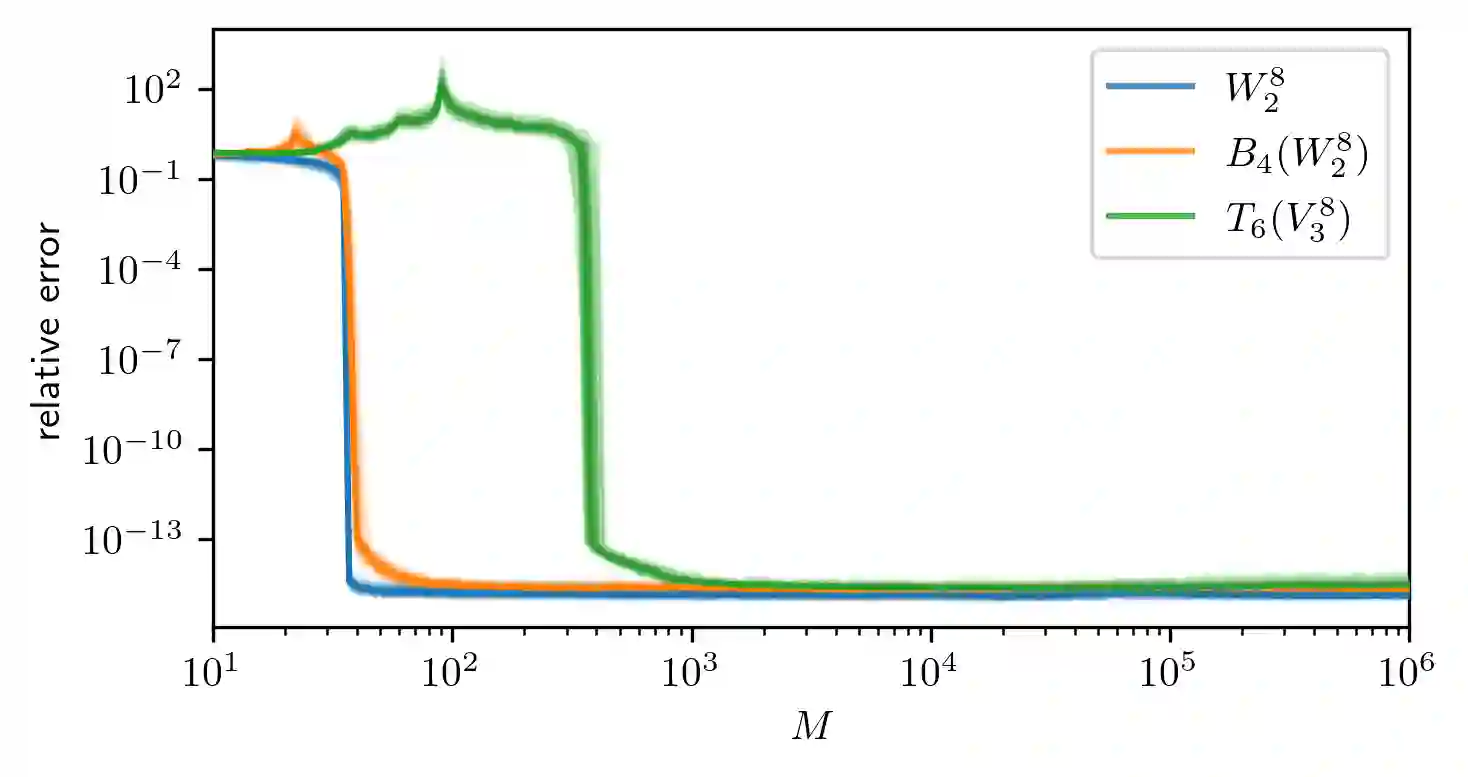
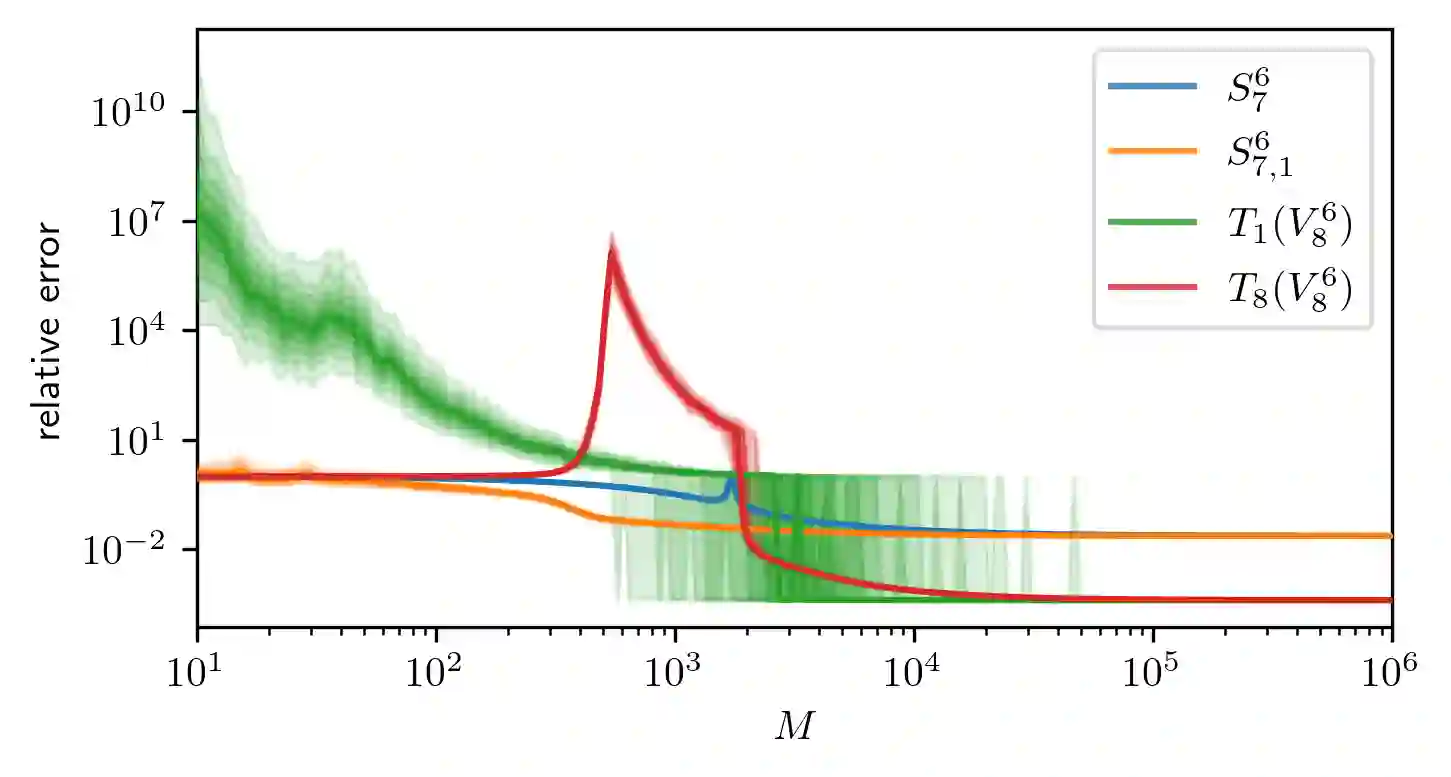
Low-rank tensors are an established framework for high-dimensional least-squares problems. We propose to extend this framework by including the concept of block-sparsity. In the context of polynomial regression each sparsity pattern corresponds to some subspace of homogeneous multivariate polynomials. This allows us to adapt the ansatz space to align better with known sample complexity results. The resulting method is tested in numerical experiments and demonstrates improved computational resource utilization and sample efficiency.
翻译:低压电压是高维最小方问题的既定框架。 我们提议扩大这一框架, 纳入区块差的概念。 在多元回归的背景下, 每个聚度模式对应一些同质多变多式多元米亚空间。 这使我们能够调整 ansatz 空间, 以更好地适应已知的样本复杂程度结果。 由此产生的方法将在数字实验中测试, 并展示更好的计算资源利用率和样本效率 。
相关内容
专知会员服务
36+阅读 · 2019年10月17日
Arxiv
0+阅读 · 2021年6月17日