Multi-Relational Algebra and Its Applications to Data Insights

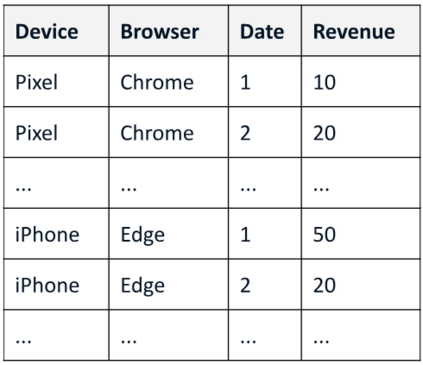
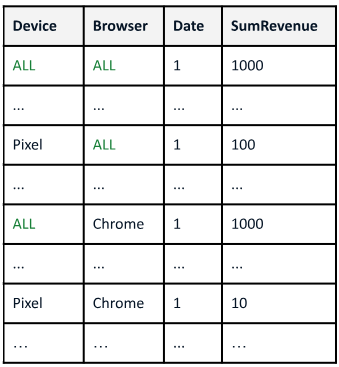
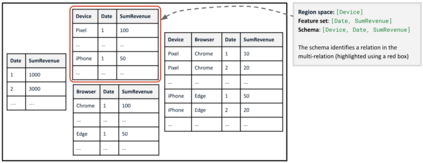
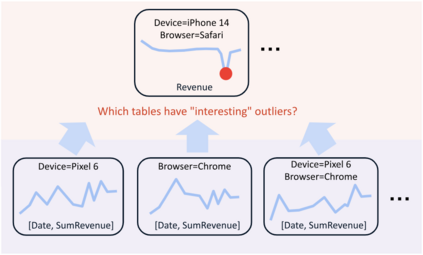
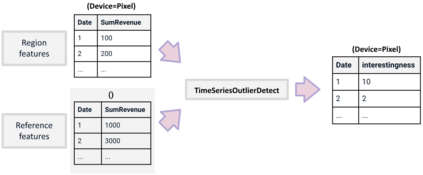
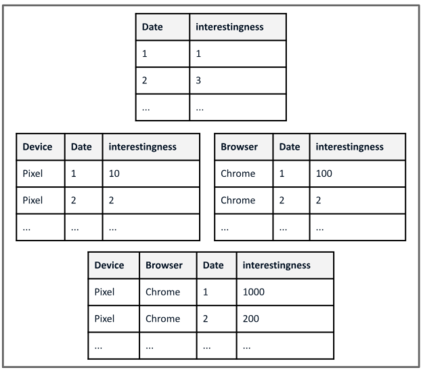
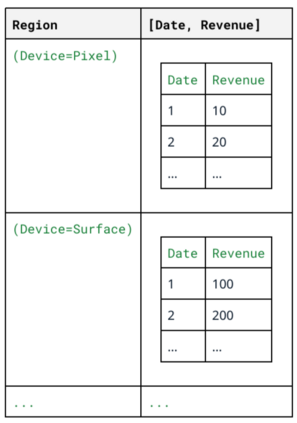
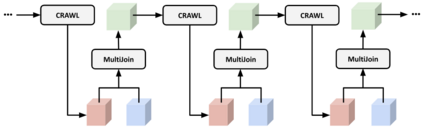
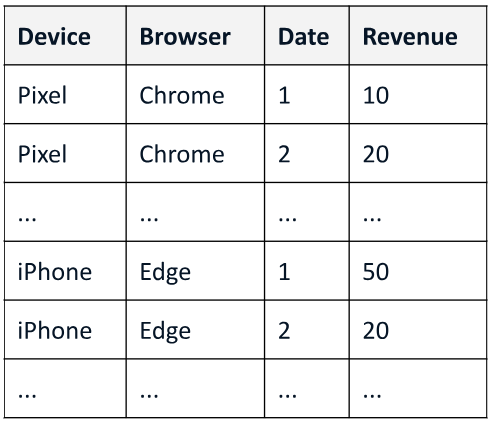
A range of data insight analytical tasks involves analyzing a large set of tables of different schemas, possibly induced by various groupings, to find salient patterns. In particular, such analyses are about many-to-many transformations of tables, while the classic relational algebra is about one-to-one or many-to-one transformations. This paper presents Multi-Relational Algebra, which extends relational algebra for such transformations and their compositions. Multi-Relational Algebra introduces MultiRelation to model of a set of tables of different schemas. Importantly, while the information unit in Relational Algebra is a tuple, the information unit in Multi-Relational Algebra is a slice, which formally is a pair $(r, X)$ where $r$ is a (region) tuple, and $X$ is a (feature) table. Multi-Relational Algebra introduces three new fundamental algebraic operators, MultiSelect, MultiProject, and MultiJoin, which lift their counterparts Select, Project, and Join to transform MultiRelation to MultiRelation. Through various examples, we show that multi-relational algebra can effortlessly express many complex analytic problems, some of which are traditionally considered out of scope for relational analytics. We have implemented and deployed a service for multi-relational analytics. Due to a unified logical design, we are able to conduct systematic optimization for a variety of seemingly different tasks. Our service has garnered interest from over a hundred internal teams who have developed data-insight applications using it, and serves millions of operators daily.