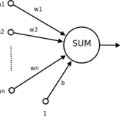
This contribution focuses on the development of Model Order Reduction (MOR) for one-way coupled steady state linear thermomechanical problems in a finite element setting. We apply Proper Orthogonal Decomposition (POD) for the computation of reduced basis space. On the other hand, for the evaluation of the modal coefficients, we use two different methodologies: the one based on the Galerkin projection (G) and the other one based on Artificial Neural Network (ANN). We aim at comparing POD-G and POD-ANN in terms of relevant features including errors and computational efficiency. In this context, both physical and geometrical parametrization are considered. We also carry out a validation of the Full Order Model (FOM) based on customized benchmarks in order to provide a complete computational pipeline. The framework proposed is applied to a relevant industrial problem related to the investigation of thermomechanical phenomena arising in blast furnace hearth walls. Keywords: Thermomechanical problems, Finite element method, Proper orthogonal decomposition, Galerkin projection, Artificial neural network, Geometric and physical parametrization, Blast furnace.
翻译:这一贡献的重点是在一定元素设置中为单向稳定的状态线性热力问题开发减少单向线性机械问题模型(MOR),我们采用适当的正正正正分解法(POD)计算缩小基空间。另一方面,在评估模型系数时,我们使用两种不同的方法:一种基于Galerkin预测(G),另一种基于人工神经网络(ANN),我们的目标是在相关特征(包括错误和计算效率)方面对POD-G和POD-ANN进行比较。在这方面,我们考虑了物理和几何对称性对称法(POD)进行适当分解法(POD),我们还根据定制基准对全序模型(FOM)进行验证,以提供一个完整的计算管道。拟议框架适用于与调查爆炸炉壁上产生的热力机械现象有关的一个相关的工业问题。关键词:热力机械问题、Finite元元素法、适当或多位解剖、Galerkin预测、人工神经网络、大地测量和物理对准。