XIGA: An eXtended IsoGeometric Analysis approach for multi-material problems

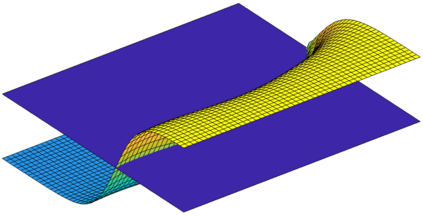
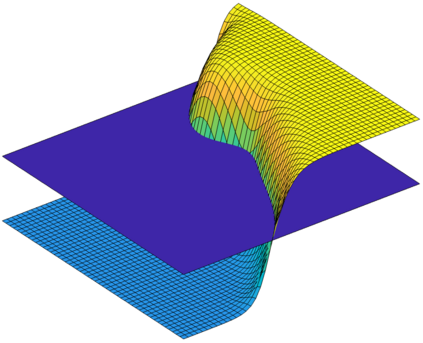
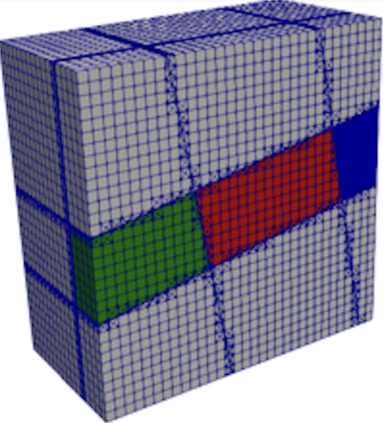
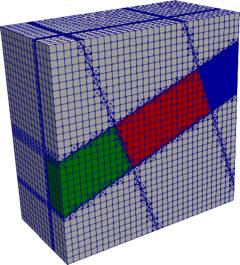
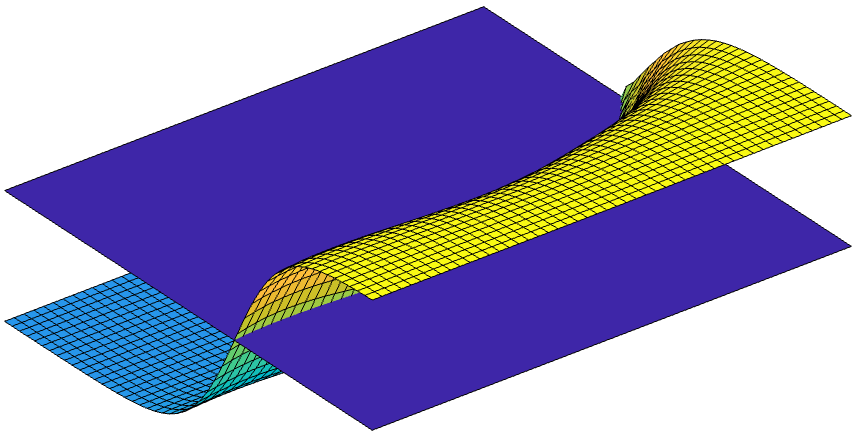
Multi-material problems often exhibit complex geometries along with physical responses presenting large spatial gradients or discontinuities. In these cases, providing high-quality body-fitted finite element analysis meshes and obtaining accurate solutions remain challenging. Immersed boundary techniques provide elegant solutions for such problems. Enrichment methods alleviate the need for generating conforming analysis grids by capturing discontinuities within mesh elements. Additionally, increased accuracy of physical responses and geometry description can be achieved with higher-order approximation bases. In particular, using B-splines has become popular with the development of IsoGeometric Analysis. In this work, an eXtended IsoGeometric Analysis (XIGA) approach is proposed for multi-material problems. The computational domain geometry is described implicitly by level set functions. A novel generalized Heaviside enrichment strategy is employed to accommodate an arbitrary number of materials without artificially stiffening the physical response. Higher-order B-spline functions are used for both geometry representation and analysis. Boundary and interface conditions are enforced weakly via Nitsche's method, and a new face-oriented ghost stabilization methodology is used to mitigate numerical instabilities arising from small material integration subdomains. Two- and three-dimensional heat transfer and elasticity problems are solved to validate the approach. Numerical studies provide insight into the ability to handle multiple materials considering sharp-edged and curved interfaces, as well as the impact of higher-order bases and stabilization on the solution accuracy and conditioning.