Gradient boosting for extreme quantile regression

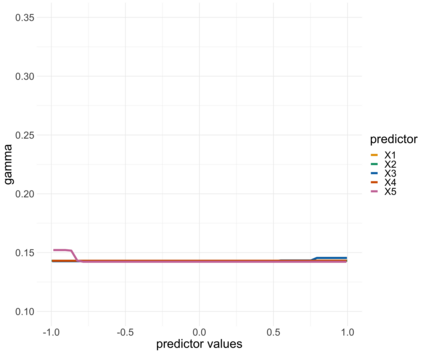
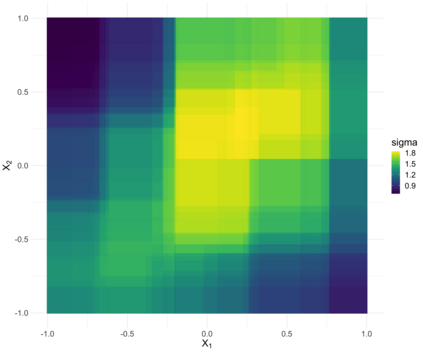
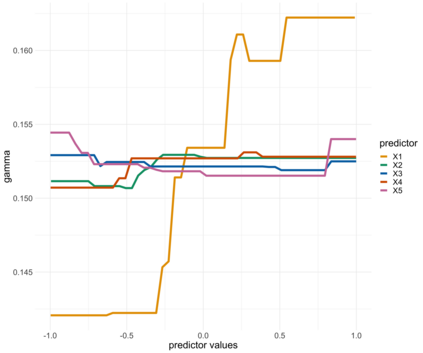
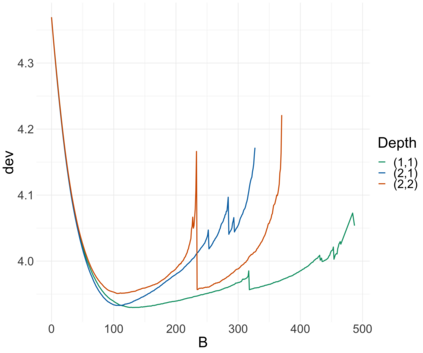
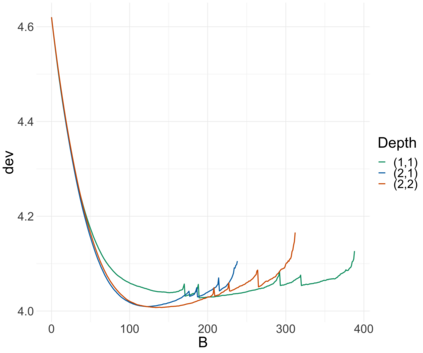
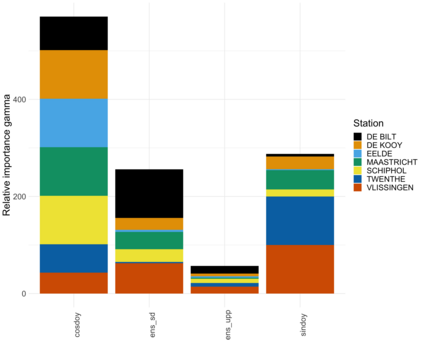
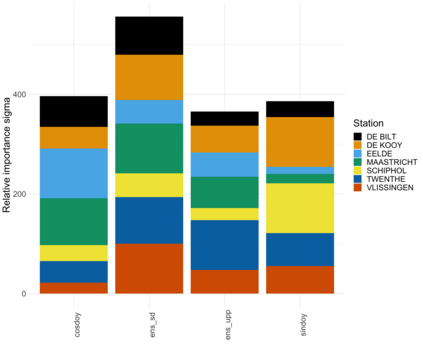
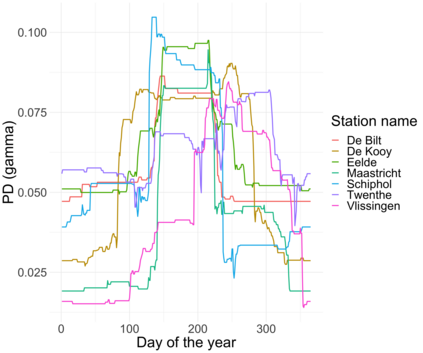
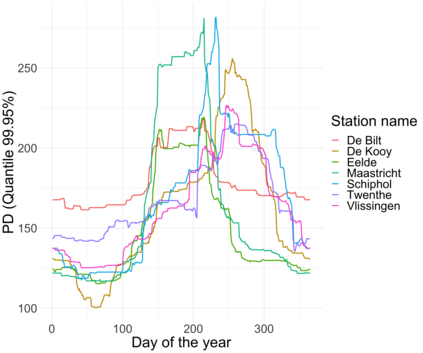
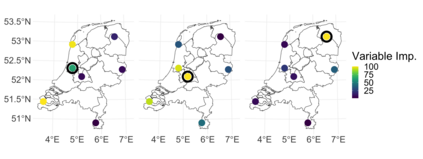
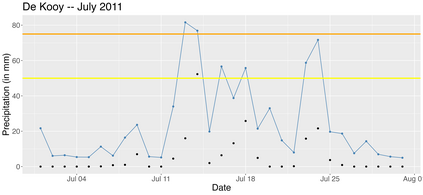
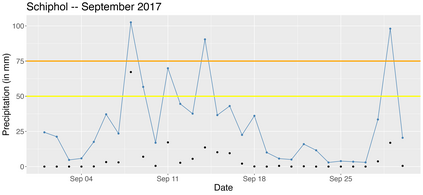
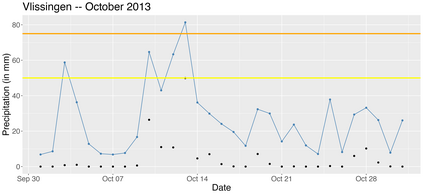
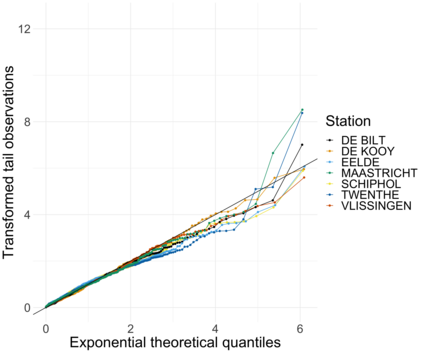
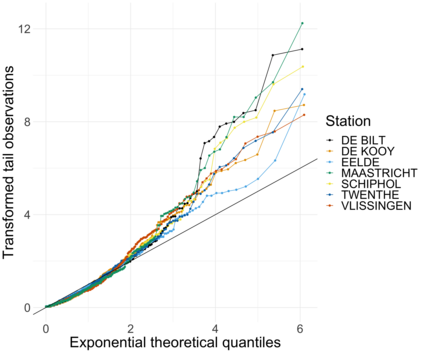
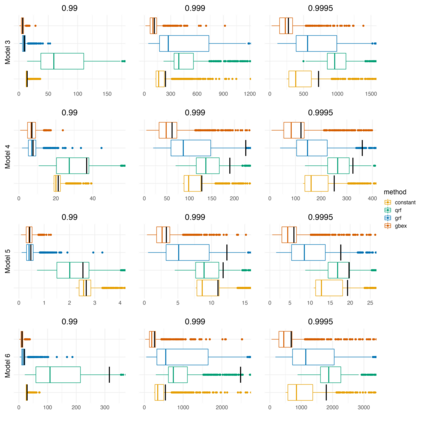
Extreme quantile regression provides estimates of conditional quantiles outside the range of the data. Classical quantile regression performs poorly in such cases since data in the tail region are too scarce. Extreme value theory is used for extrapolation beyond the range of observed values and estimation of conditional extreme quantiles. Based on the peaks-over-threshold approach, the conditional distribution above a high threshold is approximated by a generalized Pareto distribution with covariate dependent parameters. We propose a gradient boosting procedure to estimate a conditional generalized Pareto distribution by minimizing its deviance. Cross-validation is used for the choice of tuning parameters such as the number of trees and the tree depths. We discuss diagnostic plots such as variable importance and partial dependence plots, which help to interpret the fitted models. In simulation studies we show that our gradient boosting procedure outperforms classical methods from quantile regression and extreme value theory, especially for high-dimensional predictor spaces and complex parameter response surfaces. An application to statistical post-processing of weather forecasts with precipitation data in the Netherlands is proposed.