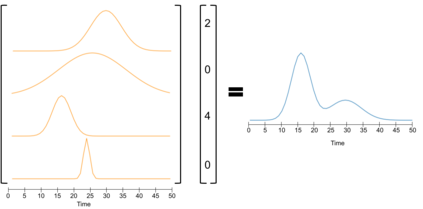
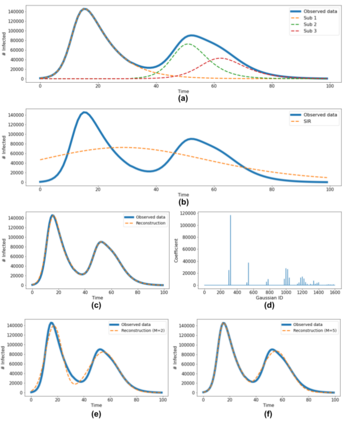
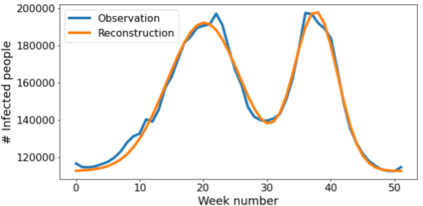
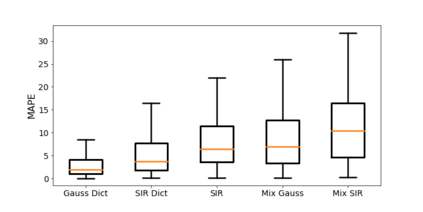
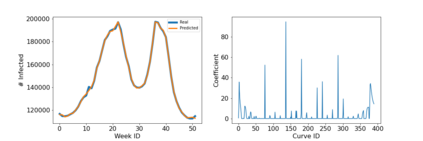
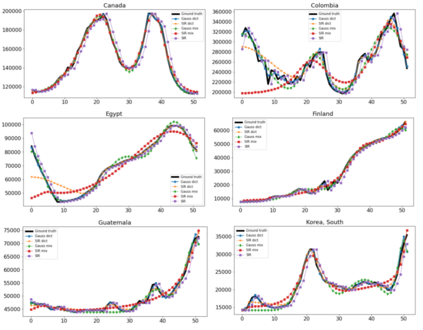
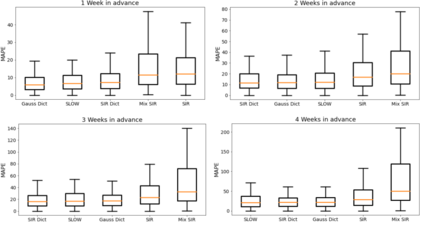
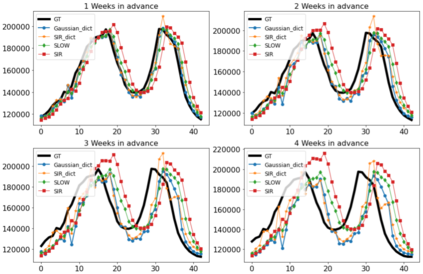
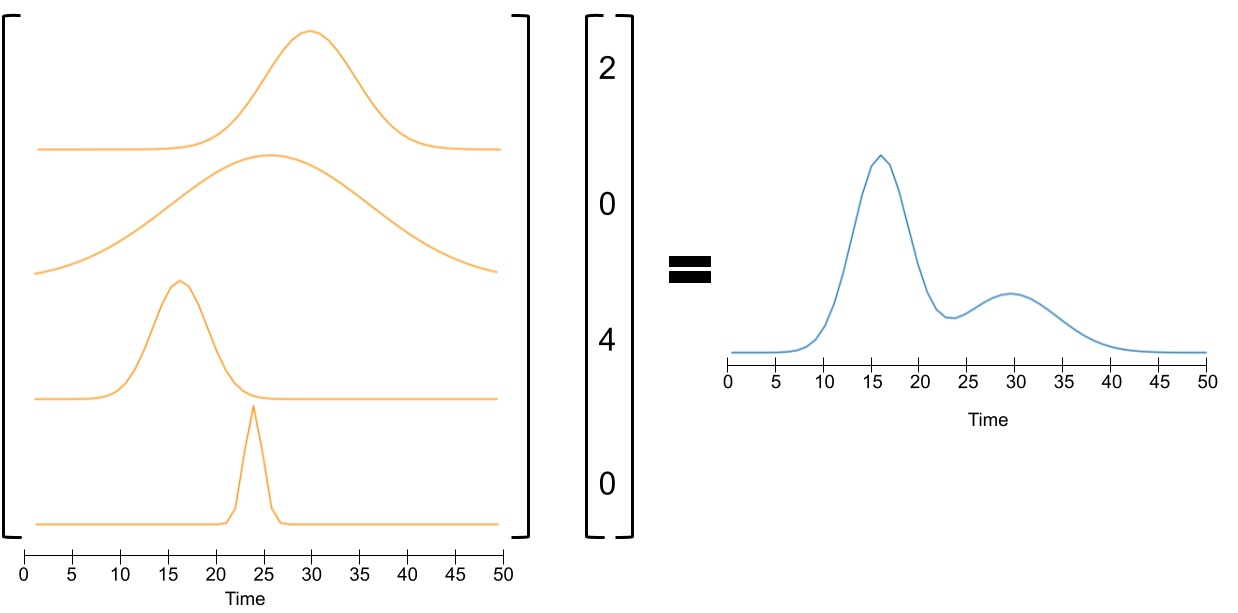
Classical epidemiological models assume homogeneous populations. There have been important extensions to model heterogeneous populations, when the identity of the sub-populations is known, such as age group or geographical location. Here, we propose two new methods to model the number of people infected with COVID-19 over time, each as a linear combination of latent sub-populations -- i.e., when we do not know which person is in which sub-population, and the only available observations are the aggregates across all sub-populations. Method #1 is a dictionary-based approach, which begins with a large number of pre-defined sub-population models (each with its own starting time, shape, etc), then determines the (positive) weight of small (learned) number of sub-populations. Method #2 is a mixture-of-$M$ fittable curves, where $M$, the number of sub-populations to use, is given by the user. Both methods are compatible with any parametric model; here we demonstrate their use with first (a)~Gaussian curves and then (b)~SIR trajectories. We empirically show the performance of the proposed methods, first in (i) modeling the observed data and then in (ii) forecasting the number of infected people 1 to 4 weeks in advance. Across 187 countries, we show that the dictionary approach had the lowest mean absolute percentage error and also the lowest variance when compared with classical SIR models and moreover, it was a strong baseline that outperforms many of the models developed for COVID-19 forecasting.
翻译:典型的流行病学模型假定了同质人口。 当已知亚群人口的身份时,例如年龄组或地理位置等, 模型不同人群的模型有重要的扩展。 这里, 我们提出两种新的方法来模拟一段时间内受COVID-19感染的人数, 每种方法都是潜在亚群的线性组合 -- -- 即当我们不知道哪个人属于哪个亚群时, 唯一的现有观测数据是所有亚群的总数。 方法1 是一种基于字典的方法, 首先是大量预先确定的亚群模式( 每一个有自己开始的时间、 形状等), 然后确定小群( 吸收的) 人数的( 积极) 重量。 方法2 是一种由潜在亚群群群组成的混合- 美元曲线, 即当我们不知道哪个人属于哪个亚群, 而唯一可用的观测是所有亚群的总数。 方法都与任何参数模型兼容; 我们在这里展示了它们的使用, 首先(a) ~ Gussian 曲线, 然后(b) 最初的 ~ SIR 曲线模型, 然后确定小群数 亚群数 亚群( ) 亚群数 ) 亚组数 的亚组数 的计算中, 显示 最低的预测方法的精确 显示 的精确 的预测方法, 我们所观察到的 的 的 和 显示的精确 4 的预测 的精确 的 的 的 的 的 。