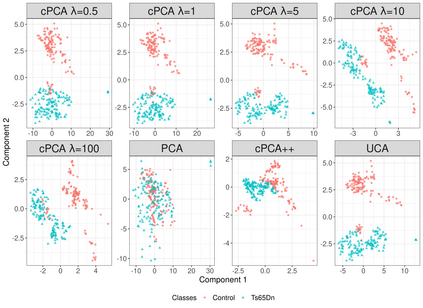
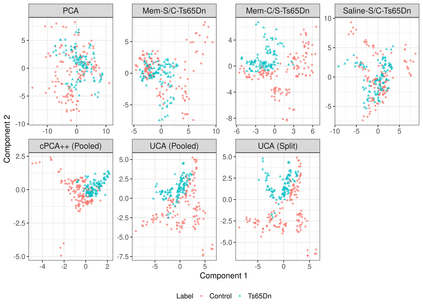
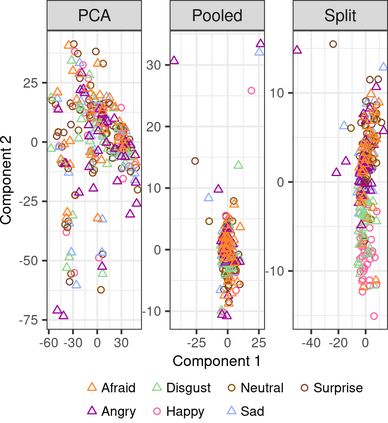
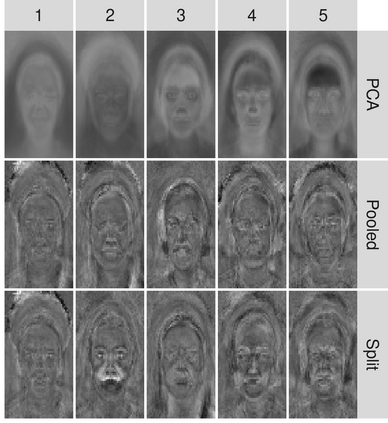
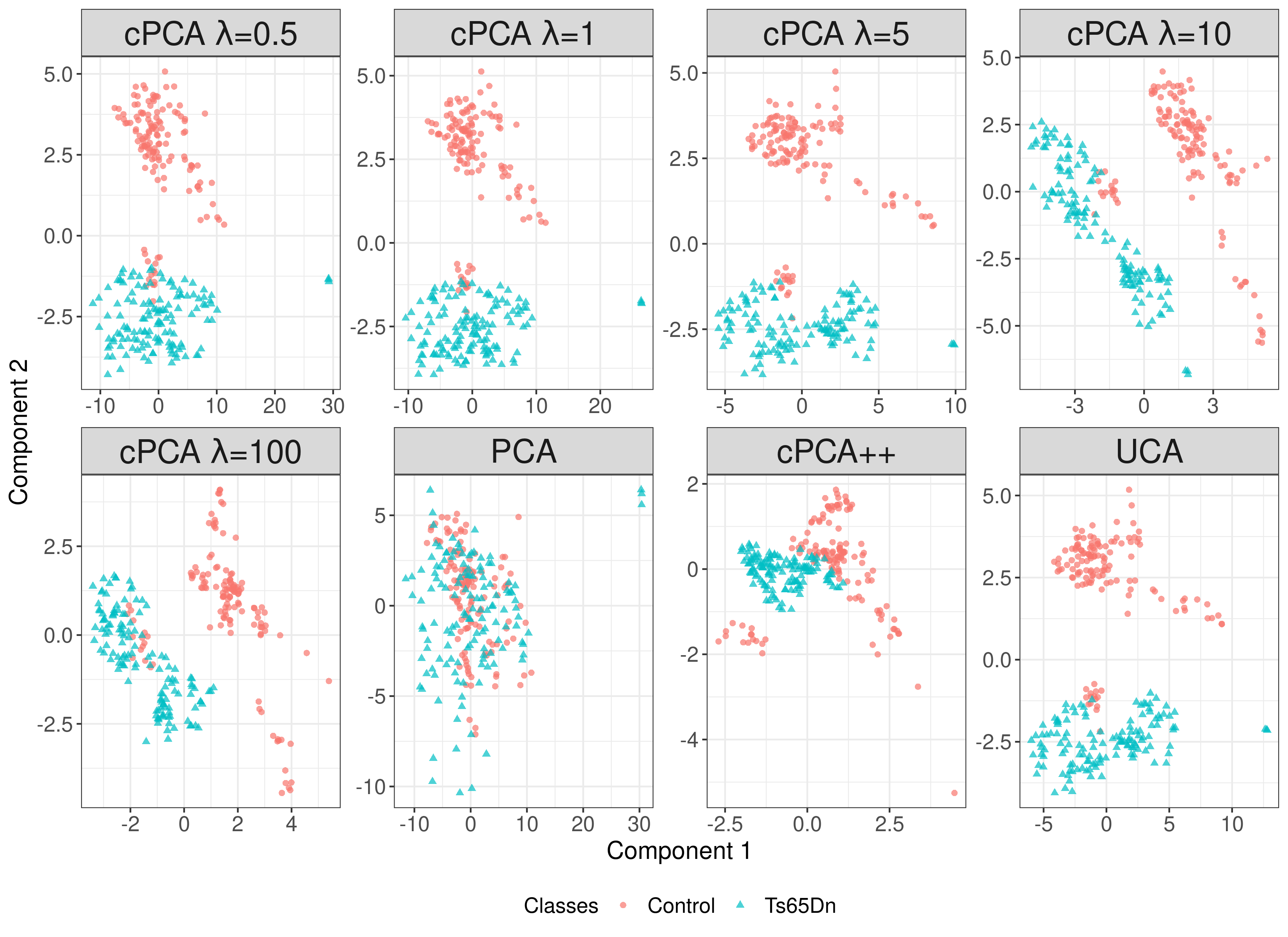
Capturing patterns of variation present in a dataset is important in exploratory data analysis and unsupervised learning. Contrastive dimension reduction methods, such as contrastive principal component analysis (cPCA), find patterns unique to a target dataset of interest by contrasting with a carefully chosen background dataset representing unwanted or uninteresting variation. However, such methods typically require a tuning parameter that governs the level of contrast, and it is unclear how to choose this parameter objectively. Furthermore, it is frequently of interest to contrast against multiple backgrounds, which is difficult to accomplish with existing methods. We propose unique component analysis (UCA), a tuning-free method that identifies low-dimensional representations of a target dataset relative to one or more comparison datasets. It is computationally efficient even with large numbers of features. We show in several experiments that UCA with a single background dataset achieves similar results compared to cPCA with various tuning parameters, and that UCA with multiple individual background datasets is superior to both cPCA with any single background data and cPCA with a pooled background dataset.
翻译:在探索性数据分析和未经监督的学习中,数据集中存在的变异模式很重要。对比性维度减少方法,例如对比性主元件分析(CPCA),通过与精心选择的背景数据集对比,发现与目标数据集有关的独特模式,显示不必要或不感兴趣的差异。然而,这类方法通常需要一个调试参数,以调节对比度,而如何客观地选择该参数则不明确。此外,与多种背景对比往往令人感兴趣,而现有方法难以完成。我们提议了一种独特的不调和的元件分析(UCA),即一种确定目标数据集相对于一个或多个比较数据集的低维度表达方式。它具有计算效率,即使具有大量特征。我们在若干实验中显示,单种背景数据集的UCA取得的结果与带有各种调试参数的CPA相似,而具有多个单个背景数据集的UCA则优于具有任何单一背景数据的PCA和具有集合背景数据集的PCA。