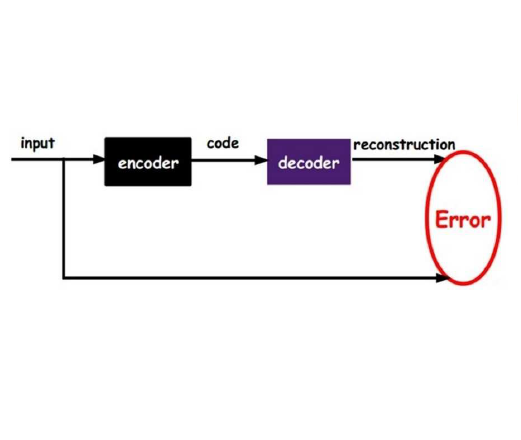
We formulate a data independent latent space regularisation constraint for general unsupervised autoencoders. The regularisation rests on sampling the autoencoder Jacobian in Legendre nodes, being the centre of the Gauss-Legendre quadrature. Revisiting this classic enables to prove that regularised autoencoders ensure a one-to-one re-embedding of the initial data manifold to its latent representation. Demonstrations show that prior proposed regularisation strategies, such as contractive autoencoding, cause topological defects already for simple examples, and so do convolutional based (variational) autoencoders. In contrast, topological preservation is ensured already by standard multilayer perceptron neural networks when being regularised due to our contribution. This observation extends through the classic FashionMNIST dataset up to real world encoding problems for MRI brain scans, suggesting that, across disciplines, reliable low dimensional representations of complex high-dimensional datasets can be delivered due to this regularisation technique.
翻译:暂无翻译