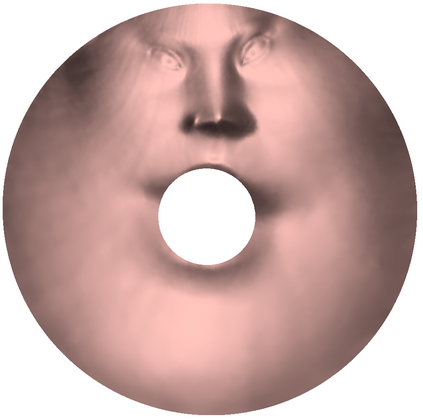
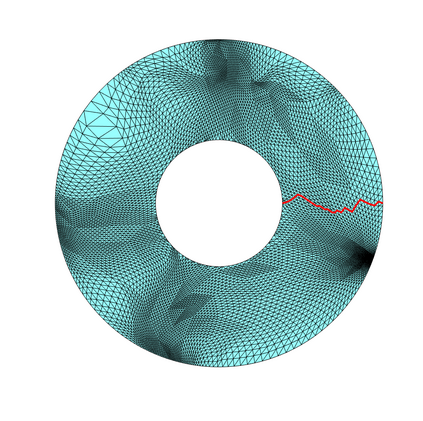
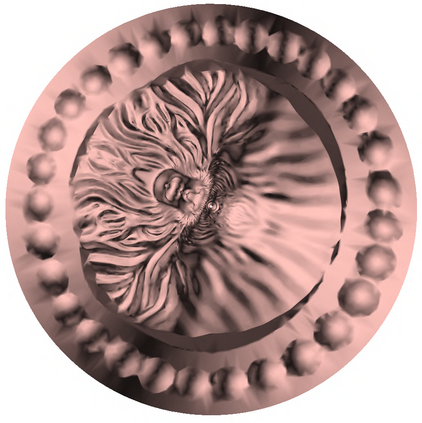
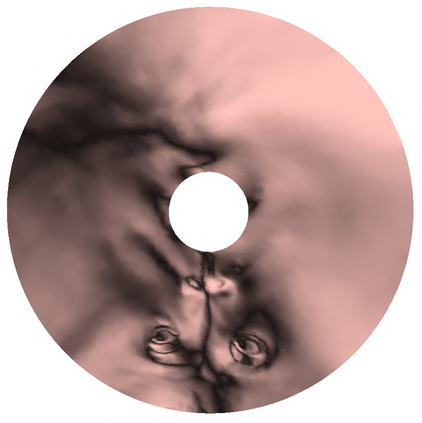
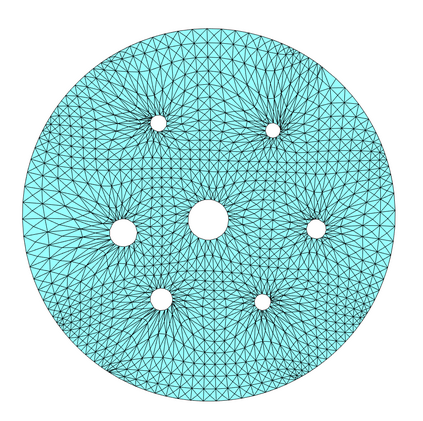
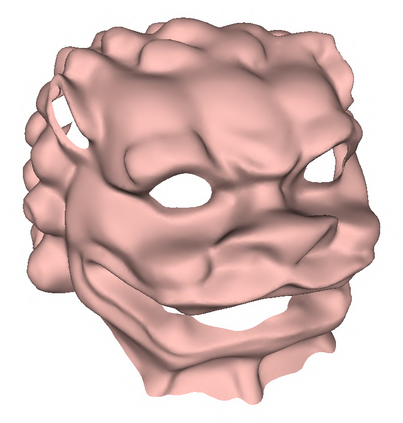
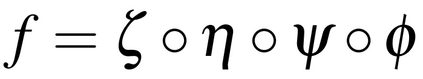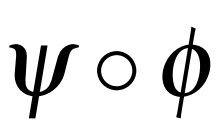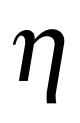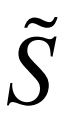Conformal mapping, a classical topic in complex analysis and differential geometry, has become a subject of great interest in the area of surface parameterization in recent decades with various applications in science and engineering. However, most of the existing conformal parameterization algorithms only focus on simply-connected surfaces and cannot be directly applied to surfaces with holes. In this work, we propose two novel algorithms for computing the conformal parameterization of multiply-connected surfaces. We first develop an efficient method for conformally parameterizing an open surface with one hole to an annulus on the plane. Based on this method, we then develop an efficient method for conformally parameterizing an open surface with $k$ holes onto a unit disk with $k$ circular holes. The conformality and bijectivity of the mappings are ensured by quasi-conformal theory. Numerical experiments and applications are presented to demonstrate the effectiveness of the proposed methods.
翻译:复杂的分析和差别几何学中的一个古典主题,即共建图谱,近几十年来已成为对地表参数化领域极为感兴趣的一个主题,在科学和工程方面有着各种应用。然而,现有的多数符合性参数化算法仅侧重于简单相连的表面,不能直接应用于有孔的表面。在这项工作中,我们提出了两种新的算法,用于计算多连接的表面的相容参数化。我们首先开发了一种有效的方法,对空面进行符合性的参数化,用一个洞对平面作废。然后,根据这种方法,我们开发了一种有效的方法,将一个有美元洞的开放表面同一块圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆的圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆的圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆