Fused graphical lasso for brain networks with symmetries

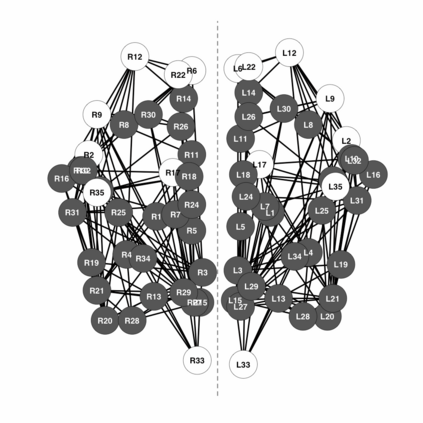
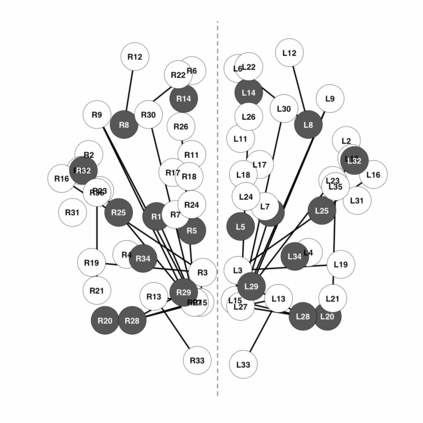
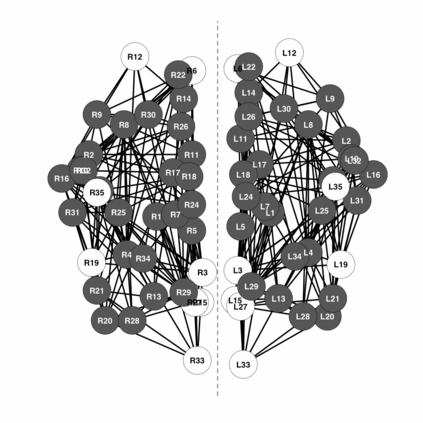
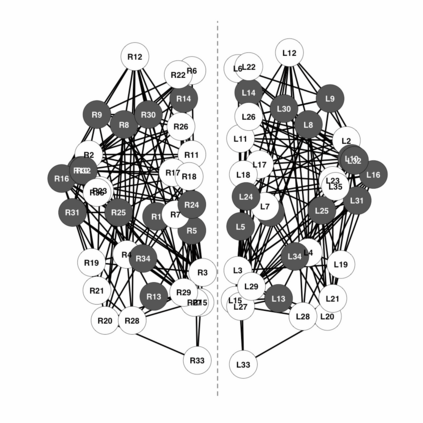
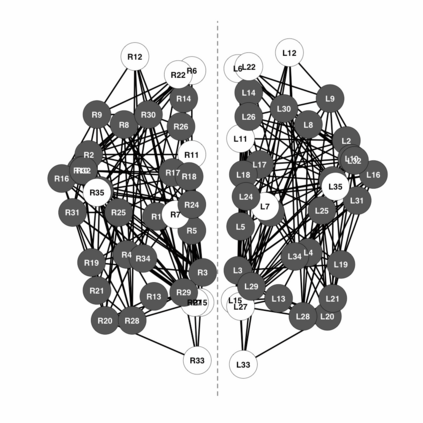
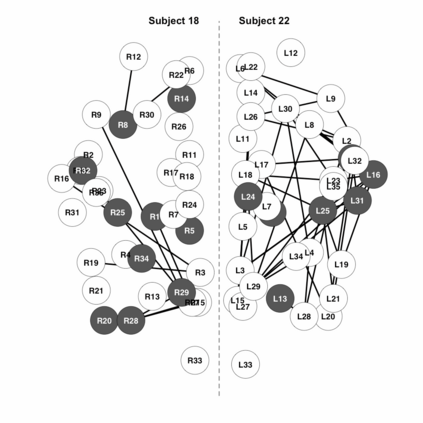
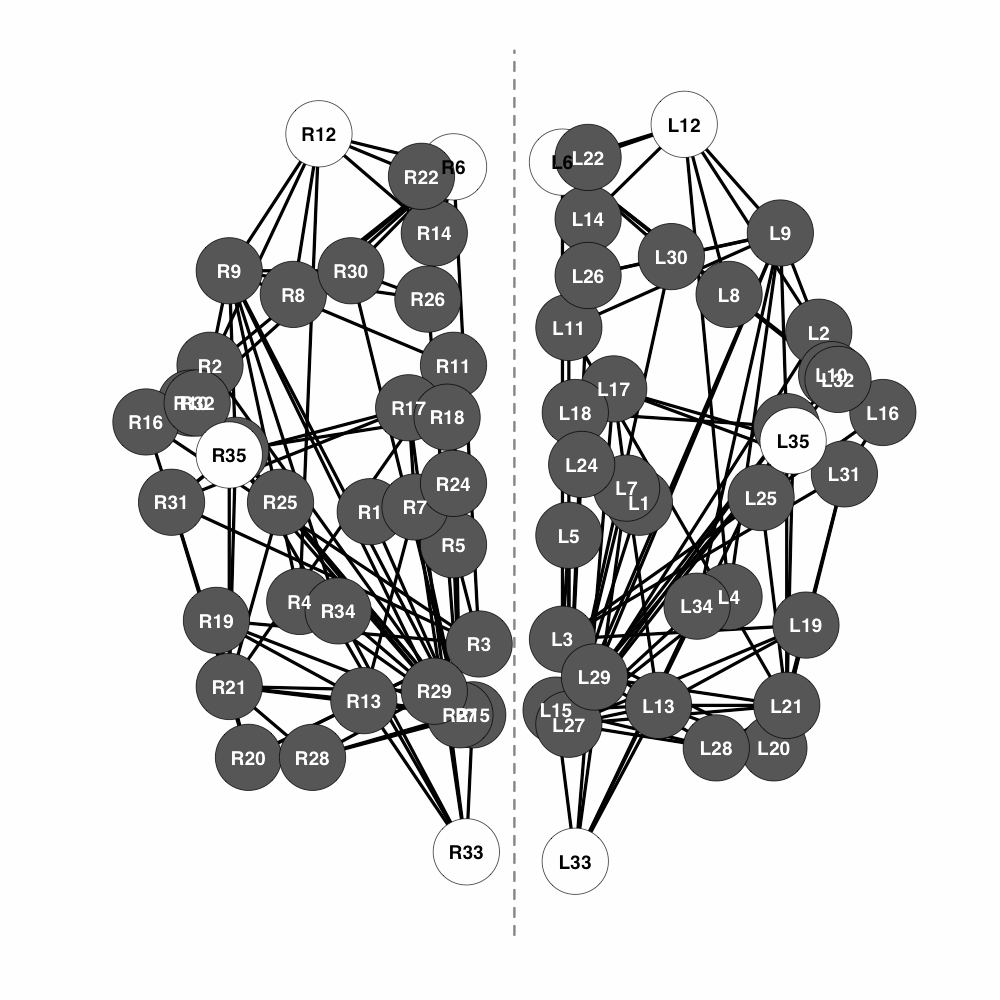
Neuroimaging is the growing area of neuroscience devoted to produce data with the goal of capturing processes and dynamics of the human brain. We consider the problem of inferring the brain connectivity network from time dependent functional magnetic resonance imaging (fMRI) scans. To this aim we propose the symmetric graphical lasso, a penalized likelihood method with a fused type penalty function that takes into explicit account the natural symmetrical structure of the brain. Symmetric graphical lasso allows one to learn simultaneously both the network structure and a set of symmetries across the two hemispheres. We implement an alternating directions method of multipliers algorithm to solve the corresponding convex optimization problem. Furthermore, we apply our methods to estimate the brain networks of two subjects, one healthy and the other affected by a mental disorder, and to compare them with respect to their symmetric structure. The method applies once the temporal dependence characterising fMRI data has been accounted for and we compare the impact on the analysis of different detrending techniques on the estimated brain networks.