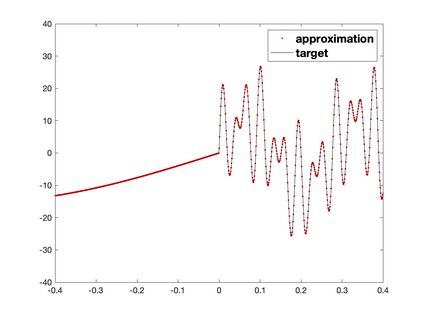
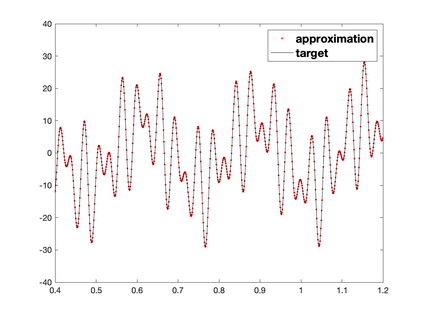
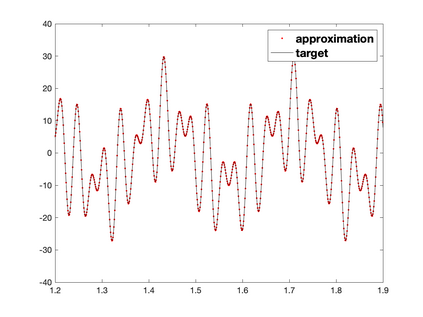
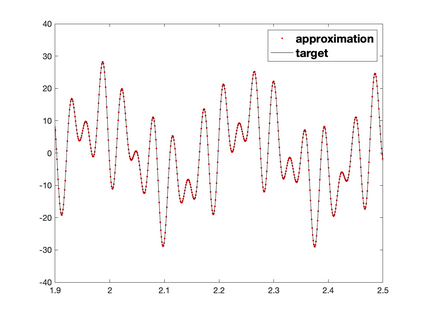
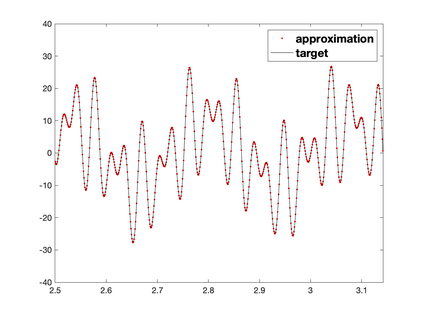
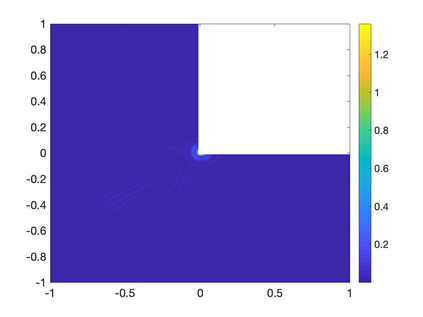
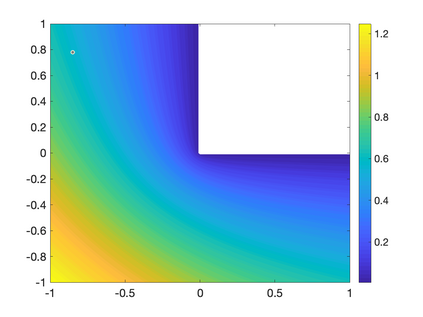
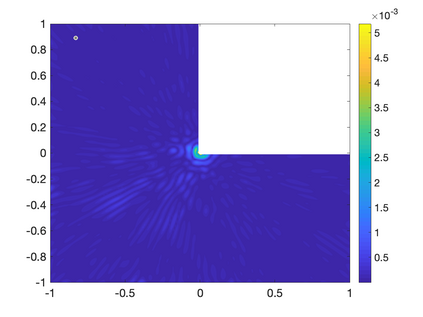
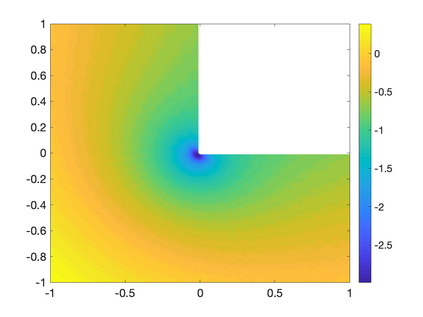
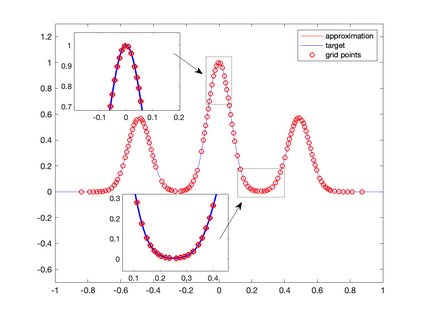
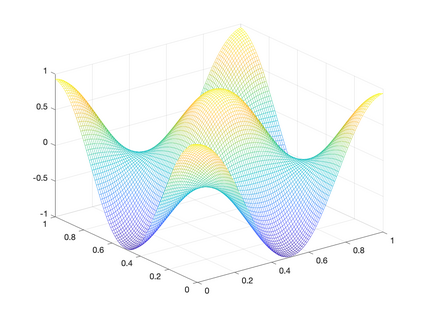
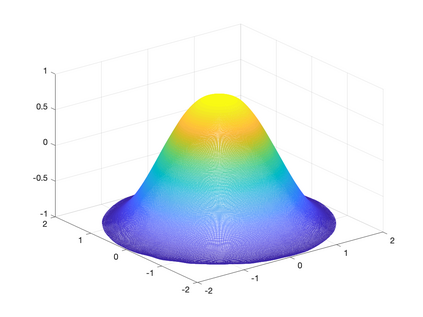
Recently, neural networks have been widely applied for solving partial differential equations. However, the resulting optimization problem brings many challenges for current training algorithms. This manifests itself in the fact that the convergence order that has been proven theoretically cannot be obtained numerically. In this paper, we develop a novel greedy training algorithm for solving PDEs which builds the neural network architecture adaptively. It is the first training algorithm that observes the convergence order of neural networks numerically. This innovative algorithm is tested on several benchmark examples in both 1D and 2D to confirm its efficiency and robustness.
翻译:最近,神经网络被广泛应用于解决部分差异方程式。然而,由此产生的优化问题给当前的培训算法带来了许多挑战。 这表现在理论上已经证明无法从数字上获得趋同顺序。 在本文中,我们开发了一种新的解决 PDE 的贪婪培训算法,以适应性的方式构建神经网络结构。这是第一个从数字上观察神经网络趋同顺序的培训算法。这个创新算法在1D和2D两个标准例子中都进行了测试,以证实其效率和稳健性。