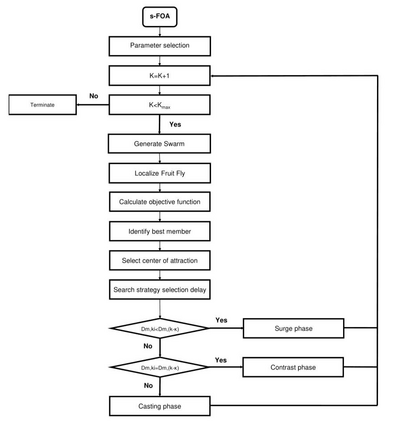
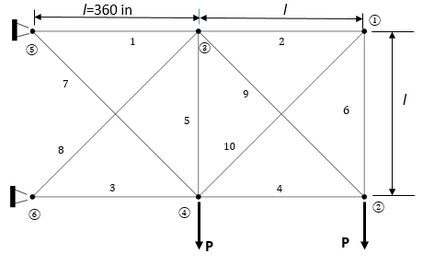
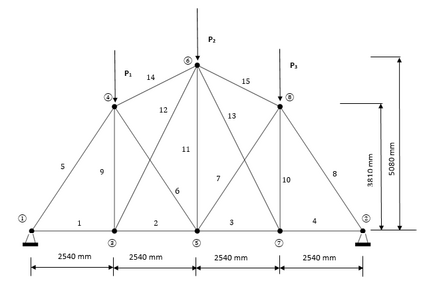
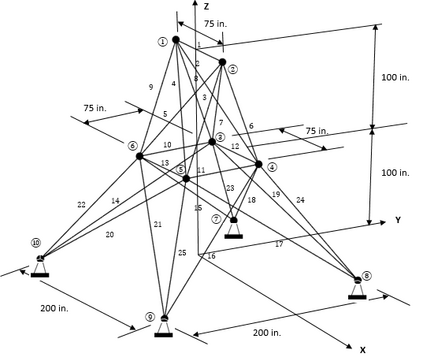
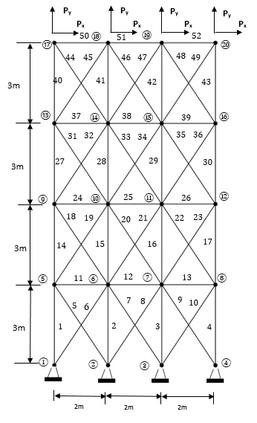
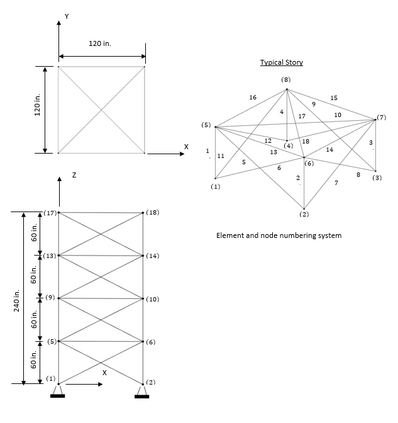
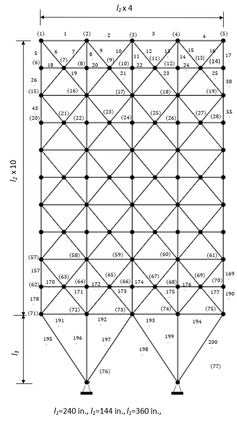
Over the past decade, several researchers have presented various optimisation algorithms for use in truss design. The no free lunch theorem implies that no optimisation algorithm fits all problems; therefore, the interest is not only in the accuracy and convergence rate of the algorithm but also the tuning effort and population size required for achieving the optimal result. The latter is particularly crucial for computationally intensive or high-dimensional problems. Contrast-based Fruit-fly Optimisation Algorithm (c-FOA) proposed by Kanarachos et al. in 2017 is based on the efficiency of fruit flies in food foraging by olfaction and visual contrast. The proposed Spontaneous Fruit Fly Optimisation (s-FOA) enhances c-FOA and addresses the difficulty in solving nonlinear optimisation algorithms by presenting standard parameters and lean population size for use on all optimisation problems. Six benchmark problems were studied to assess the performance of s-FOA. A comparison of the results obtained from documented literature and other investigated techniques demonstrates the competence and robustness of the algorithm in truss optimisation.
翻译:过去十年来,一些研究人员提出了各种优化算法,用于Turs设计;没有免费午餐理论意味着没有优化算法适合所有问题;因此,不仅对算法的准确率和趋同率感兴趣,而且对实现最佳结果所需的调整努力和人口规模也感兴趣,后者对于计算密集或高维问题尤为重要。Kanarachos等人在2017年提出的对准基于水果的优化Algorithm(c-FOA)法(c-FOA)法(c-FOA)法基于水果苍蝇在以流体和视觉对比方式进行食品饲料饲料中的效率。提议的自发性水果优化计算法(s-FOA)加强了c-FOA法(s-FOA),通过提出标准参数和精密度人口规模用于所有优化问题的解决非线优化算法的困难。研究了六个基准问题,以评估S-FOA的绩效。对文献和其他调查技术的比较表明TUs优化的算法的能力和稳健性。