A Weyl geometric approach to the gradient-flow equations in information geometry

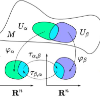
The gradient-flow equations in information geometry are reconsidered from the perspective of Weyl integrable geometry. The pre-geodesic equations associated with the gradient-flow equations are regarded as the general pre-geodesic equations in the Weyl integrable geometry.