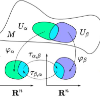
Choosing the Fisher information as the metric tensor for a Riemannian manifold provides a powerful yet fundamental way to understand statistical distribution families. Distances along this manifold become a compelling measure of statistical distance, and paths of shorter distance improve sampling techniques that leverage a sequence of distributions in their operation. Unfortunately, even for a distribution as generally tractable as the multivariate normal distribution, this information geometry proves unwieldy enough that closed-form solutions for shortest-distance paths or their lengths remain unavailable outside of limited special cases. In this review we present for general statisticians the most practical aspects of the Fisher geometry for this fundamental distribution family. Rather than a differential geometric treatment, we use an intuitive understanding of the covariance-induced curvature of this manifold to unify the special cases with known closed-form solution and review approximate solutions for the general case. We also use the multivariate normal information geometry to better understand the paths or distances commonly used in statistics (annealing, Wasserstein). Given the unavailability of a general solution, we also discuss the methods used for numerically obtaining geodesics in the space of multivariate normals, identifying remaining challenges and suggesting methodological improvements.
翻译:暂无翻译