Imputation-Free Learning from Incomplete Observations

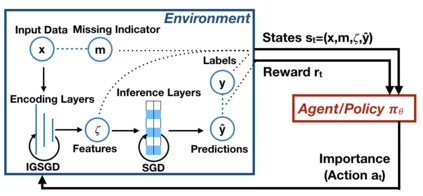
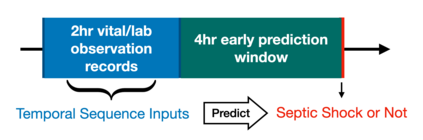
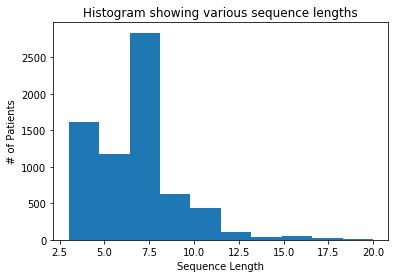
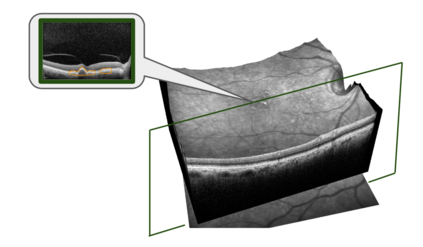
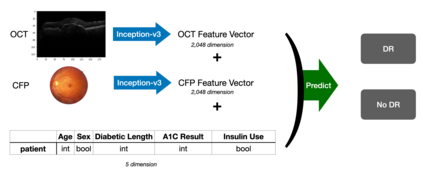
Although recent works have developed methods that can generate estimations (or imputations) of the missing entries in a dataset to facilitate downstream analysis, most depend on assumptions that may not align with real-world applications and could suffer from poor performance in subsequent tasks. This is particularly true if the data have large missingness rates or a small population. More importantly, the imputation error could be propagated into the prediction step that follows, causing the gradients used to train the prediction models to be biased. Consequently, in this work, we introduce the importance guided stochastic gradient descent (IGSGD) method to train multilayer perceptrons (MLPs) and long short-term memories (LSTMs) to directly perform inference from inputs containing missing values without imputation. Specifically, we employ reinforcement learning (RL) to adjust the gradients used to train the models via back-propagation. This not only reduces bias but allows the model to exploit the underlying information behind missingness patterns. We test the proposed approach on real-world time-series (i.e., MIMIC-III), tabular data obtained from an eye clinic, and a standard dataset (i.e., MNIST), where our imputation-free predictions outperform the traditional two-step imputation-based predictions using state-of-the-art imputation methods.