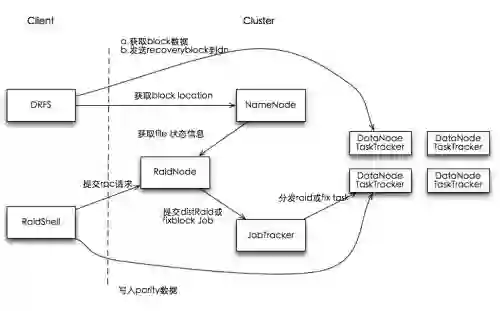
Distributed and cloud storage systems are used to reliably store large-scale data. Erasure codes have been recently proposed and used in real-world distributed and cloud storage systems such as Google File System, Microsoft Azure Storage, and Facebook HDFS-RAID, to enhance the reliability. In order to decrease the repair bandwidth and disk I/O, a class of erasure codes called locally repairable codes (LRCs) have been proposed which have small locality compare to other erasure codes. Although LRCs have small locality, they have lower minimum distance compare to the Singleton bound. Hence, seeking the largest possible minimum distance for LRCs have been the topic of many recent studies. In this paper, we study the largest possible minimum distance of a class of LRCs and evaluate them in terms of achievability. Furthermore, we compare our results with the existence bounds in the literature.
翻译:为了减少修理带宽和磁盘 I/O, 提出了一类称为本地可修复代码的去除代码。 虽然 LRC 的所在地点较小,但与 Singronton 约束区相比,它们的最低距离较低。 因此, 寻找最大可能的 LRC 最小距离是最近许多研究的主题。 在本论文中,我们研究了一组 LRC 尽可能最短的最低距离,并从可实现的角度对之进行评估。 此外, 我们比较了我们的结果和文献中存在的范围。