Stochastic Latent Transformer: Efficient Modelling of Stochastically Forced Zonal Jets

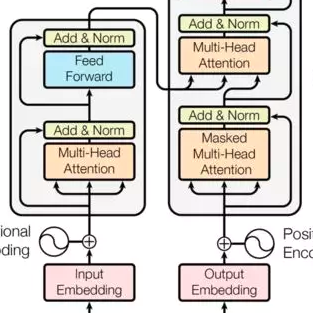
We introduce the 'Stochastic Latent Transformer', a probabilistic deep learning approach for efficient reduced-order modelling of stochastic partial differential equations (SPDEs). Despite recent advances in deep learning for fluid mechanics, limited research has explored modelling stochastically driven flows - which play a crucial role in understanding a broad spectrum of phenomena, from jets on giant planets to ocean circulation and the variability of midlatitude weather. The model architecture consists of a stochastically-forced transformer, paired with a translation-equivariant autoencoder, that we demonstrate is capable of reproducing system dynamics across various integration periods. We demonstrate its effectiveness applied to a well-researched zonal jet system, with the neural network achieving a five-order-of-magnitude speedup compared to numerical integration. This facilitates the cost-effective generation of large ensembles, enabling the exploration of statistical questions concerning probabilities of spontaneous transition events.