Semitopology: a new topological model of heterogeneous consensus

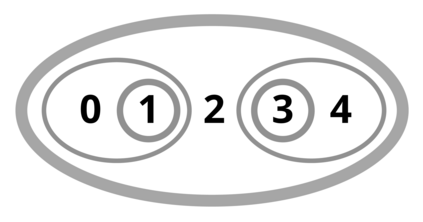
A distributed system is permissionless when participants can join and leave the network without permission from a central authority. Many modern distributed systems are naturally permissionless, in the sense that a central permissioning authority would defeat their design purpose: this includes blockchains, filesharing protocols, some voting systems, and more. By their permissionless nature, such systems are heterogeneous: participants may only have a partial view of the system, and they may also have different goals and beliefs. Thus, the traditional notion of consensus -- i.e. system-wide agreement -- may not be adequate, and we may need to generalise it. This is a challenge: how should we understand what heterogeneous consensus is; what mathematical framework might this require; and how can we use this to build understanding and mathematical models of robust, effective, and secure permissionless systems in practice? We analyse heterogeneous consensus using semitopology as a framework. This is like topology, but without the restriction that intersections of opens be open. Semitopologies have a rich theory which is related to topology, but with its own distinct character and mathematics. We introduce novel well-behavedness conditions, including an anti-Hausdorff property and a new notion of `topen set', and we show how these structures relate to consensus. We give a restriction of semitopologies to witness semitopologies, which are an algorithmically tractable subclass corresponding to Horn clause theories, having particularly good mathematical properties. We introduce and study several other basic notions that are specific and novel to semitopologies, and study how known quantities in topology, such as dense subsets and closures, display interesting and useful new behaviour in this new semitopological context.