图神经网络理论基础 | 谱图理论 Ch1: Introduction

2022 年 8 月 18 日 图与推荐

从本期开始，本专栏将开启 “谱图理论” 系列，重点围绕斯坦福大学教授、两届哥德尔奖得主 Daniel A. Spielman 所著图书 《Spectral and Algebraic Graph Theory》 （电子版链接）进行阅读探讨。本期将介绍该书第一章 Ch1: Introduction 中的内容。

本期作者 | 王涵之，中国人民大学信息学院

知乎专栏 | AlgorithmicRUC

一、图的定义及矩阵表示

1. 图的定义

图结构由节点集和边集组成，本书涉及到的图结构均为无向图，有时会涉及到权重图。图结构具有强大的关系表达能力，常被用于对真实网络结构中的实体关系进行建模。例如：好友网络中会用图节点抽象用户，用图节点之间的连边表示用户间的好友关系。类似地，通信网络中的连接关系、蛋白质网络中的相互作用关系等，都可用图节点间的连边进行建模。

2. 图的矩阵表示

图结构的表示方式有两种：邻接表和邻接矩阵。本书重点关注图的邻接矩阵以便于谱图理论分析。

2.1 Matrix as a Spreadsheet

给定图结构，其对应的邻接矩阵（adjacency matrix）为：

从表面上看，邻接矩阵是对图结构上连边关系的一种归纳，本书形象地使用“a spreadsheet”来定义邻接矩阵的这一功能。不过，正如本书中所述：“It says nothing about what it does!”，图结构中所包含的信息远多于图节点间的连边关系。

2.2 Matrix as an Operator

除了关系归纳功能（a spreadsheet），更深层次地，矩阵亦可被看作一个算子（an operator）。例如，对于矩阵，其本质上对应一个转化函数（map function），可将向量转化为向量，亦可将向量转化为一个数。不过，要想在图结构上体现出矩阵的算子特性，需要进一步定义两个矩阵：概率转移矩阵（probability transition matrix，本书中称为diffution matrix）和 拉普拉斯矩阵（Laplacian matrix）。

2.2.1 概率转移矩阵

概率转移矩阵的定义为：

其中，为图的邻接矩阵，为图的度数矩阵。邻接矩阵的定义上文已经给出，度数矩阵是一个的对角矩阵（为图中的节点数），处存储节点的度数。此处，，其中是一个全1向量。

如前所述，矩阵内含算子特性，可将向量转化为向量。图的概率转移矩阵可以很好地体现出这一特性。考虑如下过程：图上的各节点在各时刻都拥有一些物品（例如：气体），在下一时刻，图上各节点会将其当前所拥有的全部物品均匀地分配该节点的各个邻居。当然，该节点也会接收到其邻居节点传递来的物品。这是一个离散时间的离散随机过程，我们将各时刻各节点所拥有的物品数量看作该节点在该时刻的状态值，从而在图上形成了一个维的状态向量，记作。图的概率转移矩阵描述了状态向量在下一时刻的变化过程，即。

2.2.1 拉普拉斯矩阵

拉普拉斯矩阵被定义为，其中，即为图的度数矩阵，为图的邻接矩阵。

如前所述，矩阵具有算子功能，其二次型可将向量转化为一个数。在图结构上，拉普拉斯矩阵的二次型常被用于捕捉图结构的性质。具体而言，拉普拉斯矩阵的二次型为：

其中，表示边上的权重。若为无权图，则图上任意边的权重都为1。观察上式，可以看到，数值反应出向量在图结构上的平滑程度。具体而言，我们仍将看作一个状态向量，其第维的值对应图节点的状态值。图上各节点与其邻居节点间的状态值差异越小，即对于任意图节点，向量在其邻居节点间的变化越小，则数值越小。

二、谱图理论基础概述

在谱图理论中，特征向量、特征值和拉普拉斯矩阵具有举足轻重的地位。本章首先给出特征向量和特征值的定义以作回顾，接着进一步分析拉普拉斯矩阵上特征向量和特征值的性质。

2.1 特征向量/特征值的相关定义：

定义2.1【特征向量与特征值】： 若存在数值使得向量满足：

则被称为矩阵的特征向量，即被称为矩阵的特征值。

定义2.2【正定/半正定矩阵】： 如果一个矩阵是对称的，且其所有特征值均为正数，则该矩阵被称为正定矩阵（positive definite）。类似地，如果一个矩阵是对称的，且其所有特征值均非负，则该矩阵被称为半正定矩阵（positive semidefinite）。

2.2 拉普拉斯矩阵的特征向量/特征值：

如前所述，拉普拉斯矩阵在谱图理论中举足轻重。本节给出了拉普拉斯矩阵的特征向量/特征值的几个基本性质。

2.2.1 存在性

如定理2.3所示，谱定理给出了实对称矩阵上特征向量（及特征值）的存在性保证，且证明了各特征向量间的正交关系。谱定理的证明将在第二章介绍文档中给出。

值得注意的是，拉普拉斯矩阵即为实对称矩阵，故谱定理所述性质对图拉普拉斯矩阵成立。换言之，对于一个节点数为的图结构，其对应的拉普拉斯矩阵存在个相互正交的特征向量和相对应的个特征值。

为了表述的方便，本书用表示维拉普拉斯矩阵的个特征值，且不失一般性地假设。其中，常被称为拉普拉斯矩阵的最小特征值，被称为次小特征值。

定理2.3【谱定理（The Spectral Theorem）】： 若矩阵是一个的实对称矩阵，则存在实数和个相互正交的单位向量。其中，对任意，向量为矩阵的特征向量，其所对应的特征值为，即。

2.2.2 非负性

本节证明任意图结构对应的拉普拉斯矩阵的特征值均为非负的。换言之，任意图结构的拉普拉斯矩阵都是半正定矩阵。

定理2.4： 对于任意图结构，其拉普拉斯矩阵是半正定（positive semidefinite）的。

证明：为了表述的简洁性，本证明中将任意图的拉普拉斯矩阵简写为。回顾上文，拉普拉斯矩阵的二次型可被写为

进一步地，若向量是拉普拉斯矩阵的一个单位特征向量（即，为特征向量所对应的特征值），则有：

上述推导的最后一步应用了向量是单位向量（即长度为1的向量）的定义：。结合上述两式，可得：

上式证明了的非负性。注意到为拉普拉斯矩阵任一特征向量所对应的特征值，故拉普拉斯矩阵所有特征值均非负。由定义2.2，拉普拉斯矩阵为半正定矩阵。

2.2.3 平凡解

本节给出了图拉普拉斯矩阵特征值的一个平凡值，具体而言，图上拉普拉斯矩阵的定义决定了其最小特征值始终为。

定理2.5： 给定图结构，其拉普拉斯矩阵的最小特征值满足：。

证明：如上文所述，图结构的拉普拉斯矩阵。对于任意，邻接矩阵第行的行和即为节点的度数，即。换言之，拉普拉斯矩阵各行的和都为。因此，，即本是拉普拉斯矩阵的一个特征值。此处表示一个维的全1向量，亦可被替换为其他的常数向量。进一步地，由定理2.4可得，拉普拉斯矩阵所有特征值均非负，故是拉普拉斯矩阵的最小特征值（即）。

三、谱图性质与图结构

本章选取了几个特殊的图结构（如线状图、网格图、多面体图等）以展示拉普拉斯矩阵的特征向量/特征值与图结构间的相关关系。

1. 低频/高频特征值

回顾上文，对于含有个节点的图结构，其拉普拉斯矩阵的特征值由小到大依次命名为。对于较小的，常被称为低频特征值（low-frequency eigenvalues）。对应地，被称为高频特征值（high-frequency eigenvalue）。

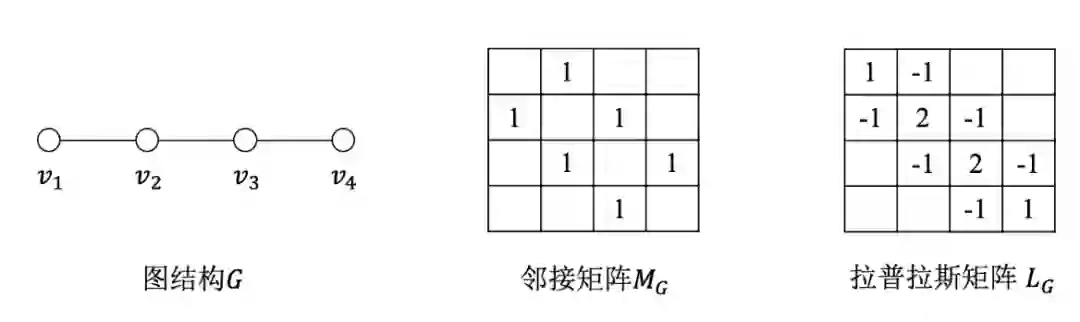
这一命名方式的背后逻辑可借助线状图结构进行直观理解。线状图（path graph）是一类特殊的图结构，其形状示意如下左图所示。更为具体的，对于一个含有个节点的线状图（即图节点集），其连边关系可表示为 ( )。换言之，线状图上的节点依次连接（第个节点与第个节点之间有一条无向边），最后得到的图结构像一条直线。下中图、下右图分别展示了节点数为4的线状图的邻接矩阵和拉普拉斯矩阵。

对于一个节点数为10的线状图，下图上方展示了图的所有特征值（即）。可以看到，最小特征值，与定理2.5所述相吻合。此外，对于次小特征值所对应的特征向量，下图左边列出了的具体取值，下图右边展示了的可视化结果（图线上第个点的横坐标即为，纵坐标为向量第维的具体取值，即）。可以看到，趋近于一条直线，即向量的各维数值依次递增，且增长幅度近似趋同。

类似地，对于一个节点数为10的线状图，下图左边展示了图特征向量的可视化结果（即与所对应的特征向量），可以看到，的震动频率逐渐增大。更为极端地，下图右边展示了的可视化结果，其各维取值的正负频繁变化，震动频率最大。

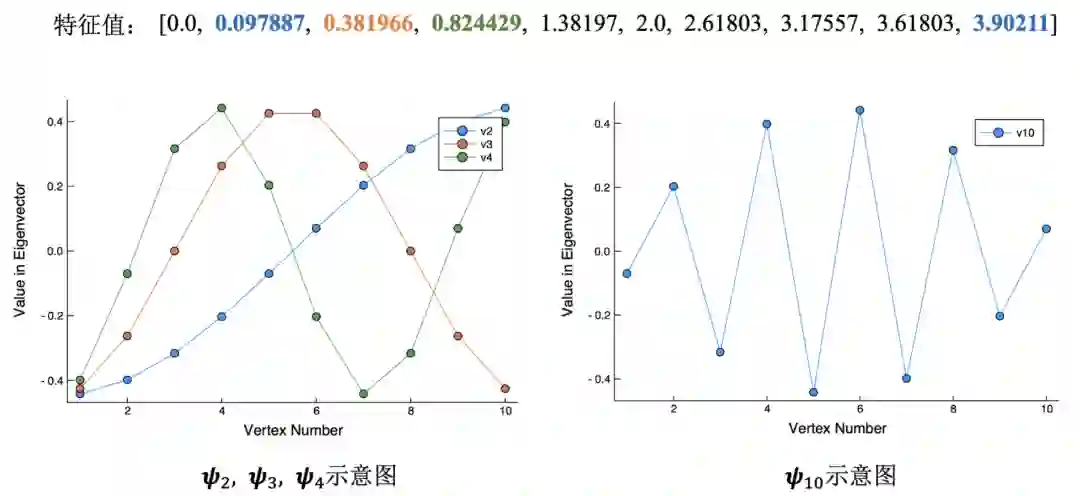
因此，对于较小的，被称为低频特征值（low-frequency eigenvalues）。而最大的则被称为高频特征值

2. 特征向量绘图

进一步地，低频特征值所对应的特征向量可用于图结构模拟。特别地，对于一个维空间的柏拉图立体（即正多面体），将其拉普拉斯矩阵的第至个特征值（即）所对应的特征向量（即）作为对应坐标系的坐标，即可得到该图结构的模拟。下文展示了二维空间的网格图和三维空间的十二面体图上，使用特征向量进行图结构绘制的结果。这一结论的严格证明请见本书第三章。

2.1 网格图（Grid Graph）

下图左侧展示了一个的网格图，下图中列展示了该网格图拉普拉斯矩阵的第2、3个特征向量（即和所对应的特征向量），下图右侧展示了的可视化结果（对应横坐标，对应纵坐标），可以看到，可以很好地模拟出一个网格图。

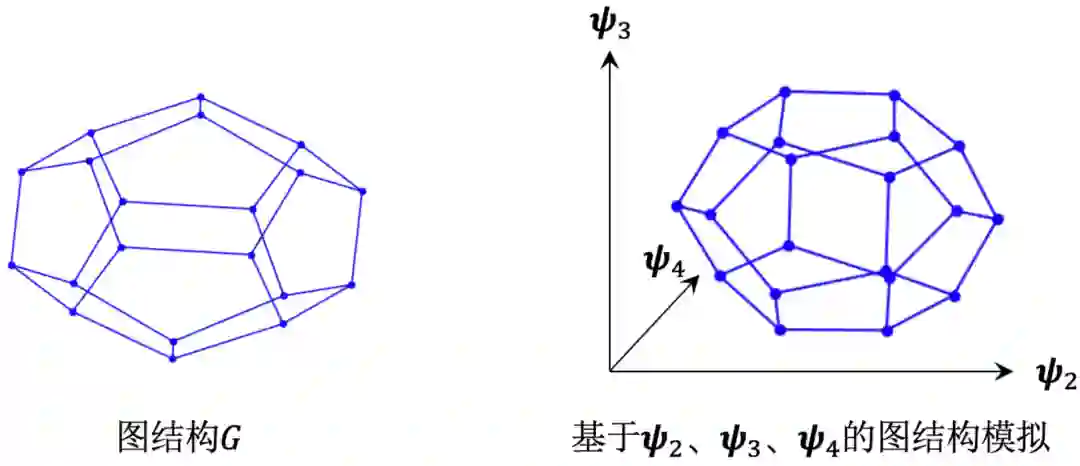
2.2 十二面体图（Dodecahedron）

上述结论可推广至所有的正立方体图。例如，对于一个十二面体图结构，下图左侧为该图结构的示意，下图右侧使用该图结构拉普拉斯矩阵的第2、3、4个特征向量进行了图绘制，所得图结构亦可较好地模拟原十二面体图结构。值得注意的是，如果正立方体图结构的可视化结果需要在维空间中展示，则需使用特征向量对该图结构进行绘制。