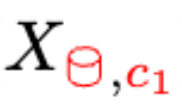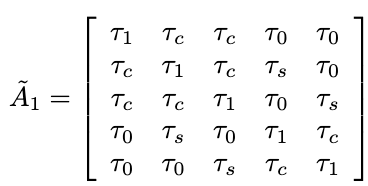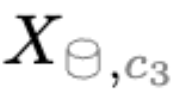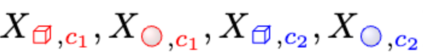Novel Class Discovery (NCD) aims at inferring novel classes in an unlabeled set by leveraging prior knowledge from a labeled set with known classes. Despite its importance, there is a lack of theoretical foundations for NCD. This paper bridges the gap by providing an analytical framework to formalize and investigate when and how known classes can help discover novel classes. Tailored to the NCD problem, we introduce a graph-theoretic representation that can be learned by a novel NCD Spectral Contrastive Loss (NSCL). Minimizing this objective is equivalent to factorizing the graph's adjacency matrix, which allows us to derive a provable error bound and provide the sufficient and necessary condition for NCD. Empirically, NSCL can match or outperform several strong baselines on common benchmark datasets, which is appealing for practical usage while enjoying theoretical guarantees.
翻译:暂无翻译